Start: Rotkäppchen und die drei Tanten
Zu Beginn ein Ausflug in die Welt der Märchen: Rotkäppchen hatte nicht nur eine Großmutter, sondern – was weniger bekannt ist – auch drei Tanten, Agathe, Beatrice und Cynthia. Diese wohnen in drei Häusern, die zusammen ein Dreieck bildeten. Wenn Rotkäppchen nicht ihre Großmutter besucht, dann besucht sie eine der drei Tanten. Letzten Sonntag jedoch war sie sehr unschlüssig, welche sie besuchen sollte. Sie startete, um Agathe einen Besuch abzustatten. Jedoch genau auf dem halben Weg zu Agathe wurde sie unsicher und überlegte es sich noch einmal. Sie beschloß, eine ihrer drei Tanten aufzusuchen, es könnte auch wieder Agathe gewesen sein. Doch es war wie verhext: Jedesmal, wenn sie genau den halben Weg zurückgelegt hatte, wurde sie wieder unsicher und entschloß sich neu, einer ihrer drei Tanten aufzusuchen, möglicherweise die gleiche, möglicherweise eine andere. Und das wieder, und wieder, und wieder …
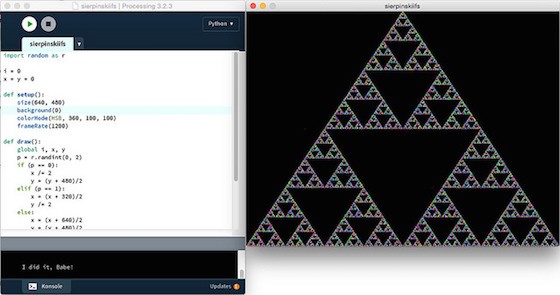
William P. Beuamont [Beaum1996] nannte es das »Tantenspiel«. Ziel ist es nicht, herauszufinden, welche Tante gewinnt (es kann gar keine gewinnen), sondern welche Figur entsteht, wenn man Rotkäppchens Irrweg visualisiert. Ich habe das einmal mit Processing.py nachprogrammiert und herausgekommen ist obige Figur, in der Fachliteratur auch als Sierpinski Dreieck bekannt, benannt nach dem polnischen Mathematiker Wacław Sierpiński, der das Fraktal schon 1915 als erster beschrieb.
Der Quellcode
Normalerweise wird dieses Fraktal mit einem rekursiven Algorithmus erzeugt, aber es geht eben auch mithilfe dieses »Chaos-Spiels« [Herrm1994]
import random as r
i = 0
x = y = 0
def setup():
size(640, 480)
background(0)
colorMode(HSB, 360, 100, 100)
frameRate(1200)
def draw():
global i, x, y
p = r.randint(0, 2)
if (p == 0):
x /= 2
y = (y + 480)/2
elif (p == 1):
x = (x + 320)/2
y /= 2
else:
x = (x + 640)/2
y = (y + 480)/2
stroke(i%360, 100, 100)
point(x, y)
i += 1
if (i > 120000):
print("I did it, Babe!")
noLoop()
Die Schleife wird 120.000 mal durchlaufen, bevor sie stoppt. Damit ich nicht ewig auf das Ergebnis warten muß, habe ich die Framerate auf 1.200 FPS gesetzt. Das ist vermutlich etwas übertrieben, in diversen Foren habe ich Vermutung gefunden, daß Processing kaum eine Framerate von 1.000 FPS überschreiten kann. Das habe ich experimentell bestätigt, obiger Sketch lief auf meinem schnellsten Rechner, einem Mac Pro mit 3,5 GHz 6-Core Intel Xeon E5, 2 Minuten und 20 Sekunden. Wären genau 1.000 FPS erreicht worden, hätte er exakt 2 Minuten laufen müssen.
Aber man sieht sehr schön, wie sich das Dreieck zufällig, aber dennoch erkennbar, zusammensetzt. Je nach zufälligem Startwert liegen die ersten drei bis vier Punkte noch außerhalb des Fraktals, danach geht aber alles seinen geordneten Gang. Und an den Farben erkennt man, daß auch die Reihenfolge, in der die einzelnen Punkte des Fraktals von Rotkäppchen angelaufen werden, ebenfalls zufällig sind.
Literatur
- [Beaum1996] William P. Beaumont: Conquering the Math Bogeyman, in Clifford A. Pickover (Ed.): Fractal Horizons – The Future Use of Fractals, New York (St. Martin's Press) 1996, Seiten 3 - 15
- [Herrm1994] Dietmar Herrmann: Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1994, Seiten 132ff.