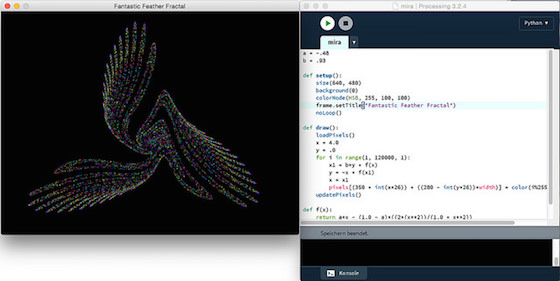
Punkte und Pixel

Punkte und Pixel sind die grundlegenden Elemente der Computergraphik. Ist man in der Lage einen Punkt auf den Monitor oder in ein Graphik-Fenster zu zaubern, dann kann man auch alle anderen graphischen Elemente erzeugen, denn diese sind im Prinzip ja auch nur eine Ansammlung von Punkten oder Pixeln. Daher beginnt meine Einführung in Processing.py mit diesen Pixeln und zeigt, was man damit schon alles anstellen kann.

Turmite

Turmiten sind quadratische, 1x1 Pixel große, kybernetische Kreaturen mit einer höchst kümmerlichen Andeutung eines Gehirns. Sie können die Farben des Pixels oder der Zelle, auf der sie gerade stehen, erkennen und danach handeln. Ist die Zelle schwarz, färben sie sie rot und bewegen sich um ein Feld nach links. Ist die Farbe rot, färben sie die Zelle schwarz und bewegen sich um ein Feld nach rechts.

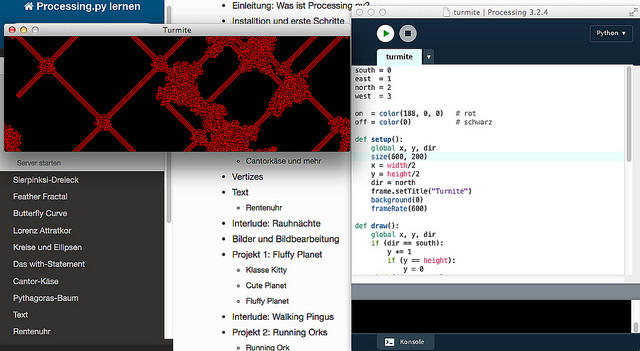
Wird solch eine Turmite auf eine schwarze, unendlichen Ebene gesetzt, erzeugt sie zuerst ein chaotisches Muster. Doch nach ungefähr 10.000 Schritten bildet sie auf einmal eine Turmiten-Autobahn, eine regelmäßige Struktur, die immer nach 104 Schritten in denselben Zustand zurückkehrt, nur jeweils um 2 Felder verschoben.

Die Turmite programmieren

Ich habe eine dieser Turmiten zum Leben erweckt. Damit sie nicht in der Unendlichkeit der Ebene entfleucht, habe ich die Ecken des Fensters miteinander verklebt und sie so in eine Torus-Welt verwandelt. Wenn die Turmite am unteren Ende des Fensters verschwindet, taucht sie am oberen Ende wieder auf, verschwindet sie am rechten Rand erscheint sie wieder am linken Rand. Für beide Ränder gilt das natürlich auch umgekehrt, die Welt der Turmite ist also ein fett aufgeblasener Fahrradschlauch, auf dem sie sich entlang bewegt.

Den Farbsensor der Turmite habe ich mit dem Processing-Befehl get(x, y) simuliert. Er liest die Farbe des Pixels. Analog dazu gibt es die Funktion set(x, y, color), die die Farbe color an die Stelle x, y schreibt. Die beiden Farben habe ich im Sketch on für schwarz und off für rot genannt. Ich bin von der Metapher ausgegangen, daß die Turmite auf der schwarzen Ebene ein Feld entweder einschaltet (also rot färbt) oder es wieder ausschaltet (es wird wieder schwarz).

Als ich in den späten 1980er Jahren auf meinem Atari-ST mein erstes Turmitenprogramm schrieb, dauerte es ewig, bis die Turmite mit ihrer Autobahn im Unendlichen verschwunden war (sie das Bildschirmfenster verlassen hatte). An eine Rückkehr via Torus wagte ich nicht zu denken, dafür reichte meine Geduld nicht aus. Nun in Processing.py habe ich die Framerate auf 600 gesetzt und so geht es doch recht schnell voran.

Interessant ist, daß die Turmite, wenn sie auf eine von ihr geschaffene Autobahn trifft, zwar erst einmal wieder ein chaotisches Verhalten an den Tag legt, aber über kurz oder lang wieder eine Autobahn baut. Diese Turmiten-Autobahnen kennen nur zwei Orientierungen, sie verlaufen entweder parallel oder stehen senkrecht aufeinander.

Quellcode

Nach dem oben Beschriebenen dürfte der Quellcode leicht verständlich sein. In der setup()-Funktion wird die Hintergrundfarbe auf schwarz und die Turmite in die Mitte des Fensters mit der Ausrichtung nach Norden gesetzt.

Im ersten Abschnitt der draw()-Funktion wird die Turmite gemäß Ihrer aktuellen Orientierung bewegt und die Behandlung der Fensterränder berücksichtigt. Dann wird die Farbe der aktuellen Zelle gelesen (mit get(x, y)) und je nach Zustand eine neue Farbe gesetzt und die Orientierung der Turmite den Regeln entsprechend geändert. Das ist alles.

south = 0
east  = 1
north = 2
west  = 3

on  = color(188, 0, 0)   # rot
off = color(0)           # schwarz

def setup():
    global x, y, dir
    size(600, 200)
    x = width/2
    y = height/2
    dir = north
    background(0)
    frameRate(600)

def draw():
    global x, y, dir
    if (dir == south):
        y += 1
        if (y == height):
            y = 0
    elif (dir == east):
        x += 1
        if (x == width):
            x = 0
    elif (dir == north):
        if (y == 0):
            y = height - 1
        else:
            y -= 1
    elif (dir == west):
        if (x == 0):
            x = width - 1
        else:
            x -= 1

    if (get(x, y) == on):
        set(x, y, off)
        if (dir == south):
            dir = west
        else:
            dir -= 1
    else:
        set(x, y, on)
        if (dir == west):
            dir = south
        else:
            dir += 1

Weitere mögliche Experimente

Die Turmiten gehen auf Greg Turk zurück, der damals Doktorand an der Universität von North Carolina in Chapel Hill war. Er zeigte, daß sie eine zweidimensionale Turingmaschine sind. Später hat sie Christopher Langton weiterentwickelt und beschrieben – daher ist sie auch unter dem Namen »Langtons Ameise« (Lanton's Ant) bekannt. Die hier vorgestellte ist die einfachste Form solch einer Ameise. Ein nächster Schritt wäre beispielsweise, die Welt mit zwei Turmiten zu bevölkern, die eine färbt die Ebene rot, wenn sie auf ein schwarzes Feld trifft, die andere färbt sie blau. Natürlich müßten dann beide Ameisen auch Regeln implementiert bekommen, wie sie zu verfahren haben, wenn sie auf ein blaues respektive ein rotes Feld treffen.

Von Turk selber gibt es zum Beispiel eine Turmite mit zwei Zuständen, nennen wir diese A und B und mit folgendem Regelsatz:

Zustand	A	B
grün	schwarz, vorwärs, B	grün, rechts, A
schwarz	grün, links, A	grün, rechts, A

Sie erzeugt ein Spiralmuster, »immer größer werdende strukturierte Gebiete, die sich in regelmäßiger Anordnung um einen Startpunkt winden«.

Eine weitere Turmite, die mit vier Farben hantiert, braucht nur einen Zustand, um ebenfalls ein interessantes, symmetrisches Muster zu bilden. Hier ihr Regelsatz:

Zustand	A
blau	rot, rechts, A
rot	gelb, rechts, A
gelb	grün, links, A
grün	blau, links, A

Es gibt also noch viel zu entdecken in der Welt der Turmiten und Ameisen.

Literatur

• A.K. Dewdney: Turmiten, in: Immo Diener (Hg.): Computer-Kurzweil 2, Spektrum Akademischer Verlag: Verständliche Forschung, Heidelberg 1992, Seiten 156-160
• Ameise (Turingmaschine) in der Wikipedia.

Barnsleys Farn mit Processing.py

Michael Barnsley hatte 1985 auf der SIGGRAPH ein von John Hutchinson schon 1981 erfundenes Verfahren vorgestellt, mit dem er ein Bild eines Farnkrauts mit nur vier affinen Abbildungen erzeugen konnte. Dieses Verfahren nannte er »Iteriertes Funktionssystem« (IFS). Es erregte recht goßes Aufsehen, weil man mit diesem Verfahren nicht nur andere Blätter und Bäume, sondern auch viele der klassischen Fraktale nachbilden konnte (wobei die stochastische IFS-Version streng genommen nur eine Abwandlung des Chaos-Spiels zu Anfang dieses Kapitels ist).

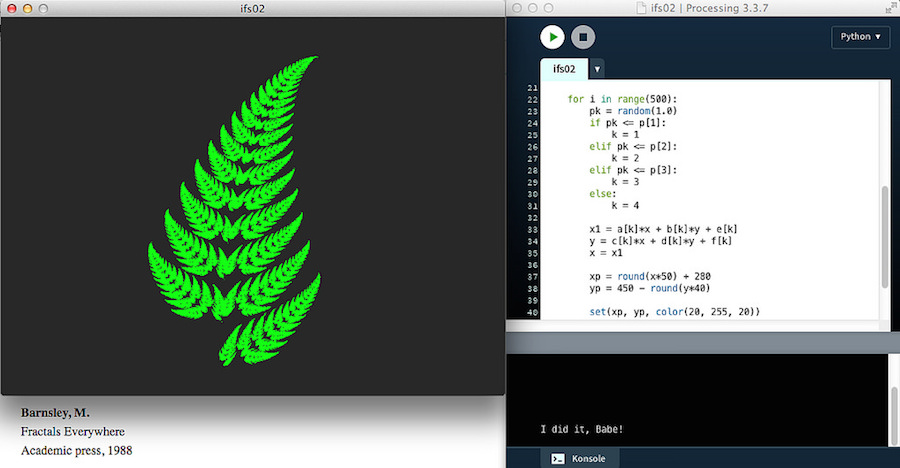
Ich habe aus nostalgischen Gründen diesen stochastischen Algorithmus auch einmal in Processing.py nachimplementiert:

# Parameter
a = [0.0, 0.197, -0.155, 0.849]
b = [0.0, -0.226, 0.283, 0.037]
c = [0.0, 0.226, 0.26, -0.037]
d = [0.16, 0.197, 0.237, 0.849]
e = [0.0, 0.0, 0.0, 0.0]
f = [0.0, 1.6, 0.14, 1.6]

# Zufallsverteilung
p = [0.03, 0.14, 0.27, 1.0]
# p = [0.074, 0.08, 0.09, 1.0]
def setup():
    global x, y
    x, y = 0.0, 0.0
    size(640, 480)
    background(40, 40, 40)

def draw():
    global x, y

    for i in range(500):
        pk = random(1.0)
        if pk <= p[1]:
            k = 1
        elif pk <= p[2]:
            k = 2
        elif pk <= p[3]:
            k = 3
        else:
            k = 4

        x1 = a[k]*x + b[k]*y + e[k]
        y = c[k]*x + d[k]*y + f[k]
        x = x1

        xp = round(x*50) + 280
        yp = 450 - round(y*40)

        set(xp, yp, color(20, 255, 20))

    if frameCount >= 500:
        print("I did it, Babe!")
        noLoop()

Eine Besonderheit in diesem Sketch ist dabei die Schleife for in range(500) in der draw()-Funktion. Denn läßt man bei jedem Durchlauf nur einen Punkt zeichnen, dauert es ganz schön lange, bis so etwas wie ein Farnblatt sichtbar wird. Denn man braucht mindestens 75.000 Punkte, um auch nur schwach etwas erkennen zu können. Mithilfe dieser Schleife aber lasse ich bei jedem Durchlauf 500 Punkte berechnen und zeichnen. Das beschleunigt das Verfahren doch enorm, so daß man in endlicher Zeit zu einem vorzeigbanren Ergebnis kommt.

Die Parameter für diesen Farn habe ich dem hier schon mehrfach erwähnten Buch »Algorithmen für Chaos und Fraktale« von Dietmar Herrmann (S. 177ff.) entnommen, das 1994 bei Addison-Wesley erschienen ist. Dort finden Sie auch noch weitere Beispiele.

Wir backen uns ein Mandelbrötchen

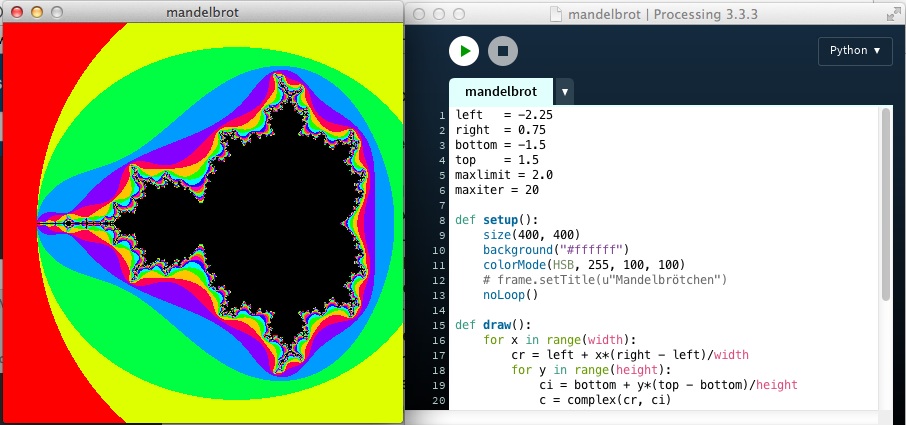
Die Mandelbrot-Menge ist die zentrale Ikone der Chaos-Theorie und das Urbild aller Fraktale. Sie ist die Menge aller komplexen Zahlen \(c\), für welche die durch

$$ \begin{align} z_{0} & = 0\\ z_{n+1} & = z_{n}^{2}+c\\ \end{align} $$

rekursiv definierte Folge beschränkt ist. Bilder der Mandelbrot-Menge können erzeugt werden, indem für jeden Wert des Parameters \(c\), der gemäß obiger Rekursion endlich bleibt, ein Farbwert in der komplexen Ebene zugeordnet wird.

Die komplexe Ebene wird in der Regel so dargestellt, daß in der Horizontalen (in der kartesisschen Ebene die x-Achse) der Realteil der komplexen Zahl und in der Vertikalen (in der kartesischen Ebene die y-Achse) der imaginäre Teil aufgetragen wird. Jede komplexe Zahl entspricht also einen Punkt in der komplexen Ebene. Die zur Mandelbrotmenge gehörenden Zahlen werden im Allgemeinen schwarz dargestellt, die übrigen Farbwerte werden der Anzahl von Iterationen (maxiter) zugeordnet, nach der der gewählte Punkt der Ebene einen Grenzwert (maxlimit) verläßt. Der theoretische Grenzwert ist 2.0, doch können besonders bei Ausschnitten aus der Menge, um andere Farbkombinationen zu erreichen, auch höhere Grenzwerte verwendet werden. Bei Ausschnitten muß auch die Anzahl der Iterationen massiv erhöht werden, um eine hinreichende Genauigkeit der Darstellung zu erreichen.

Das Programm

Python kennt den Datentyp complex und kann mit komplexen Zahlen rechnen. Daher drängt sich die Sprache für Experimente mit komplexen Zahlen geradezu auf. Zuert werden mit cr und ci Real- und Imaginärteil definiert und dann mit

c = complex(cr, ci)

die komplexe Zahl erzeugt. Für die eigentliche Iteration wird dann – nachdem der Startwert z = 0.0 festgelegt wurde – nur eine Zeile benötigt:

z = (z**2) + c

Wie schon in anderen Beispielen habe ich für die Farbdarstellung den HSB-Raum verwendet und über den Hue-Wert iteriert. Das macht alles schön bunt, aber es gibt natürlich viele Möglichkeiten, ansprechendere Farben zu bekommen, beliebt sind zum Beispiel selbsterstellte Paletten mit 256 ausgesuchten Farbwerten, die entweder harmonisch ineinander übergehen oder bestimmte Kontraste betonen.

Der komplette Quellcode

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5
maxlimit = 2.0
maxiter = 20

def setup():
    size(400, 400)
    background("#ffffff")
    colorMode(HSB, 255, 100, 100)
    noLoop()

def draw():
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = 0.0
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    set(x, y, color(0, 0, 0))
                else:
                    set(x, y, color((i*48)%255, 100, 100))

Um zu sehen, wie sich die Farben ändern, kann man durchaus mal mit den Werten von maxlimit spielen und diesen zum Beispiel auf 3.0 oder 4.0 setzen. Auch die Erhöhung der Anzahl der Iterationen maxiter verändert die Farbzuordnung, verlängert aber auch die Rechhenzeit drastisch, so daß man speziell bei Ausschnitten aus der Mandelbrotmenge schon einige Zeit auf das Ergebnis warten muß.

Pixel-Array versus set()

Will man einzelne Pixel im Ausgabefenster oder in einem Bild manipulieren, bietet Processing(.py) grundsätzlich zwei Möglichkeiten: Zum einen kann man mit

set(x, y, color)

direkt einen Farbpunkt an eine bestimmte Position x, y setzen, oder aber man lädt mit

loadPixels()

das gesamte Ausgabe-Fenster in ein eindimensionales Pixel-Array, um dann mit

pixels[x + y*width] = color()

die Farbe an die gewünschte Stelle x, y zu setzen. Anschließend darf man nicht vergessen, mit

updatePixels()

Processing dazu zu bewegen, die geänderten Pixel auch anzuzeigen. Dadurch, daß das Pixel-Array eindimensional ist und so die gewünschte Position mit x + y*width angesprochen werden muß, ist die erste Version (für die es übrigens auch noch ein entsprechendes get(x, y) gibt, mit dem man die Farbe an der gewünschten Stelle abfragen kann) einfacher handzuhaben, aber die Reference zu Processing zu bedenken:

Setting the color of a single pixel with set(x, y) is easy, but not as fast as putting the data directly into pixels[].

Das gilt aber nicht immer, mit dem im letzten Abschnitt gebackenen Mandelbrötchen habe ich die Probe aufs Exempel gemacht. Zwei nahezu identische Programme habe ich gegeneinander antreten lassen.

Programm 1: Mandelbrot-Menge mit set()

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5
maxlimit = 4.0
maxiter = 100

def setup():
    size(600, 600)
    background("#ffffff")
    colorMode(HSB, 255, 100, 100)
    noLoop()

def draw():
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = complex(0.0, 0.0)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    set(x, y, color(0, 0, 0))
                else:
                    set(x, y, color((i*48)%255, 100, 100))
    println(millis())

Programm 2: Mandelbrot-Menge mit Pixel-Array

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5
maxlimit = 4.0
maxiter = 100

def setup():
    size(600, 600)
    background("#ffffff")
    colorMode(HSB, 255, 100, 100)
    noLoop()

def draw():
    loadPixels()
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = complex(0.0, 0.0)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    pixels[x + y*width] = color(0, 0, 0)
                else:
                    pixels[x + y*width] = color((i*48)%255, 100, 100)
    updatePixels()
    println(millis())

Und – Überraschung! – das Programm mit set() war fast immer geringfügig schneller als das Programm mit den Pixel-Arrays. Auf meinem betagten MacBook Pro benötigte das erste Programm rund 15.000 bis 16.000 Millisekunden, während das zweite Programm um die 18.000 Millisekunden benötigte. Der Unterschied ist nicht groß, aber dennoch bemerkenswert. Es liegt zum einen sicher daran, daß die benötigte Zeit für die Berechnung des Apfelmännchens im Vergleich zu der benötigten Zeit, dieses zu zeichnen, riesig ist. Zum anderen wird die draw()-Schleife ja auch nur einmal durchlaufen und so kann das Pixel-Array seine Fähigkeit der schnellen Pixelmanipulation nicht richtig ausspielen.

Die Erkenntnis daraus: Es kann sich durchaus lohnen, auch mal das Handbuch zu hinterfragen.

Julia-Menge

Die Julia-Menge wurde 1918 von den beiden französischen Mathematikern Gaston Maurice Julia (nachdem sie benannt wurde) und Pierre Fatou (dessen Zugang heute die meisten Lehrbücher folgen) unabhängig voneinander beschrieben. Sie steht im engen Zusammenhang zur im letzten Abschnitt beschriebenen Mandelbrot-Menge. Während die Mandelbrot-Menge, die Menge aller komplexen Zahlen \(c\) ist, die der iterierten Gleichung

$$ \begin{align} z_{0} & = 0\\ z_{n+1} & = z_{n}^{2}+c\\ \end{align} $$

folgen, ist bei der Julia-Menge \(c\) konstant:

$$ \begin{align} z_{n}^{2}+c \end{align} $$

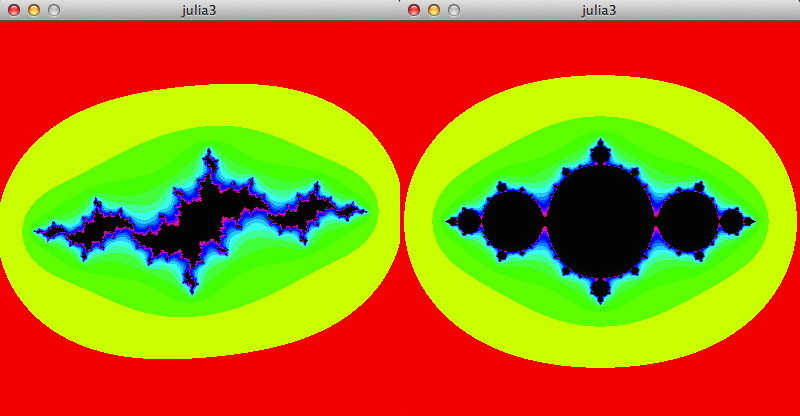
Die Mandelbrot-Menge ist also eine Beschreibungsmenge aller Julia-Mengen. Jedem Punkt \(c\) der komplexen Zahlenebene entspricht eine Julia-Menge. Eigenschaften der Julia-Menge lassen sich an der Lage von \(c\) relativ zur Mandelbrot-Menge beurteilen: Wenn der Punkt \(c\) Element der Mandelbrot-Menge ist, dann ist die Julia-Menge zusammenhängend. Andernfalls ist sie eine Cantormenge unzusammenhängender Punkte. Ist der Imaginärteil \(c_i = 0\), dann ist die Julia-Menge symmetrisch (vlg. Abbildung links oben), ansonsten kann sie alle möglichen Formen annehmen.

Julia-Menge interaktiv

Ich habe die obigen Bilder mit diesem Programm erzeugt, daß den Parameter \(c\) in Abhängigkeit von der Mausposition setzt:

left   = -2.0
right  = 2.0
bottom = 2.0
top    = -2.0
maxlimit = 3.0
maxiter = 25

def setup():
    size(400, 400)
    background("#555ddd")
    colorMode(HSB, 1)

def draw():
    cr = map(mouseX, 0, width, left, right)
    ci = 0
    # ci = map(mouseY, 0, height, top, bottom)
    c = complex(cr, ci)
    for x in range(width):
        zr = left + x*(right - left)/width
        for y in range(height):
            zi = bottom + y*(top - bottom)/height
            z = complex(zr, zi)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter-1):
                    set(x, y, color(0))
                else:
                    set(x, y, color(sqrt(float(i)/maxiter), 100, 100))
    println("cr = " + str(cr))
    println("ci = " + str(ci))

Kommentiert man die Zeile ci = 0 aus und aktiviert stattdessen die auskommentierte Zeile darunter, erhält man (theoretisch) alle Julia-Mengen, sonst erzeugt das Programm nur die symmetrischen. Richtig flüssig ist die Animation allerdings nicht, Processing.py gerät – zumindest auf meinem betagten MacBook Pro – schon ganz schön ins Stottern.

Julia-Menge animiert

Das gilt auch für das zweite Programm, das die Parameter der Julia-Menge anhand zweier Sinus- (wahlweise auch Cosinus-) Funktionen periodisch durchläuft:

left   = -2.0
right  = 2.0
bottom = 2.0
top    = -2.0
maxlimit = 3.0
maxiter = 25

def setup():
    size(400, 400)
    background("#555ddd")
    colorMode(HSB, 1)

def draw():
    # cr = 0
    cr = 2*sin(frameCount)
    ci = 0
    # ci = 2*cos(frameCount)
    c = complex(cr, ci)
    for x in range(width):
        zr = left + x*(right - left)/width
        for y in range(height):
            zi = bottom + y*(top - bottom)/height
            z = complex(zr, zi)
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter-1):
                    set(x, y, color(0))
                else:
                    set(x, y, color(sqrt(float(i)/maxiter), 100, 100))
    println("cr = " + str(cr))
    println("ci = " + str(ci))

Auch hier kommt das Programm ganz schön ins Schwitzen. Das läßt allerdings dem Betrachter Zeit, die Schönheit der Julia-Menge zu bewundern.

Noch einmal das Pixel-Array

In den letzten beiden Abschnitt habe ich gezeigt, daß Processing.py zwar relativ schnell ist, aber 120.000 Operationen in einem Bildfenster doch eine gewisse Zeit benötigen. Falls man jedoch auf die Animation verzichten kann (und damit auf point() oder get() und set()), geht es auch wesentlich schneller: Jedes Bild in Processing(.py) – und das schließt das Graphikfenster ein – wird intern als eine eindimensionale Liste der Farbwerte gespeichert. Die erste Position der Liste ist das erste Pixel links oben, die letzte Position folgerichtig das letzte Pixel rechts unten.

Ein pixels[]-Array in Processing speichert in dieser Form die Farbwerte für jedes Pixels des Ausgabefensters. Um es zu initialisieren, muß vor der ersten Nutzung die Funktion loadPixels() aufgerufen werden. Manipulationen im Pixel-Array werden erst sichtbar, wenn die Funktion updatePixels() aufgerufen wird. loadPixels() und updatePixels() bilden so ein ähnliches Geschwisterpaar von Funktionen, wie zum Beispiel beginShape() und endShape(). Doch einen Unterschied gibt es: Wird das Pixel-Array nur zum Lesen der Farbwerte genutzt, muß updatePixels() natürlich nicht aufgerufen werden. Da die Manipulationen eines Pixel-Arrays nur im Hauptspeicher des Rechners stattfinden, sind sie natürlich viel schneller als jede andere Processing-Funktion, die Bildinformationen manipuliert.

Da das Pixel-Array ein eindimensionales Array ist, muß auf die Zeilen und Spalten mit einem kleinen Trick zugegriffen werden. Jeder Punkt (x, y) steht im Pixelarray an der Position x + (y*width). An die Farbwerte eines Pixels kommt man mit dem Aufruf

i = x + (y*width)
color(c) = pixels[i]

Die einzelnen Farbwerte im RGB-Raum kann man danach so auslesen:

r = red(c)
g = green(c)
b = blue(c)

Das Setzen eines Pixels erfolgt genau umgekehrt:

pixel[i] = color(r, g, b)

Natürlich kann man auch jeden anderen Farbraum (Graustufen, HSV), den Processing kennt, nutzen.

Wie ich jedoch bei der Mandelbrotmenge gezeigt habe, ist die Manipulation über das Pixel-Array nicht automatisch schneller. Wenn die Zeiten für die Berechnung des Pixelwertes so hoch sind, daß der Geschwindigkeitsgewinn durch ein Pixel-Array vernachlässigbat ist, dann ist auch die Bildmanipulation durch das Pixel-Array nicht immer die beste Lösung.

Bei Filtern für Photos oder ähnliche Bild-Manipulationen ist jedoch ein Pixel-Array in der Regel das Werkzeug der Wahl.

Fantastic Feather Fractal

Um zu zeigen, wie schnell die Manipulationen eines Pixel-Arrays sind, möchte ich wieder eine Iteration über 120.000 Schritte durchführen. Als Demonstrationsobjekt habe ich das Fantastic Feather Fractal gewählt, das Clifford A. Pickover in seinem Buch »Mazes for the Mind« vorgestellt hat. Wenn Ihr untenstehenden Quellcode laufen laßt, werdet Ihr feststellen, daß das fertige Fraktal fast unmittelbar nach dem Aufruf im Graphikfenster erscheint.¹

Das Feather Fractal ist ein »seltsamer Attraktor«, ein Attraktor eines dynamischen Systems, das sich zwar chaotisch verhält, aber dennoch eine kompakte Menge ist, die es nie verläßt. Die Parameter des Sketches entstammen der oben genannten Quelle von Pickover, die Faktoren um das Ergebnis dem Bildfenster anzupassen habe ich durch wildes Herumexperimentieren gefunden².

Der Quellcode

a = -.48
b = .93

def setup():
    size(640, 480)
    background(0)
    colorMode(HSB, 255, 100, 100)
    frame.setTitle("Fantastic Feather Fractal")
    noLoop()

def draw():
    loadPixels()
    x = 4.0
    y = .0
    for i in range(1, 120000, 1):
        x1 = b*y + f(x)
        y = -x + f(x1)
        x = x1
        pixels[(350 + int(x*26)) + ((280 - int(y*26))*width)] = color(i%255, 100, 100)
    updatePixels()

def f(x):
    return a*x - (1.0 - a)*((2*(x**2))/(1.0 + x**2))

Wenn ich später noch auf Bildmanipulationen in Processing zurückkomme, werden die Pixel-Arrays noch einmal ausführlich behandelt werden.

Literatur

• Clifford A. Pickover: Mazes for the Mind. Computers and the Unexpected, New York (St. Martin's Press) 1992. Das Buch gehört zu den Besten des umtriebigen Autors und da es aufgrund seines Alters antiquarisch für ein paar Cent zu bekommen ist, sollten Sie zuschlagen. Das Feder-Fraktal ist auf den Seiten 33f. beschrieben, die über 400 anderen Seiten erfüllen fast jeden Traum eines an Computer-Experimenten interessierten Menschen.
• Florian Freistetter: Best of Chaos: Der seltsame Attraktor, Science Blogs (Astrodicticum Simplex) vom 4. Februar 2015 (Ich bin ein Fan von Florian Freistetter, er ist einer der wenigen guten deutschsprachigen Erklärbären für Naturwissenschaften.)