Shapes

For Your Eyes Only – Processing.py zieht Kreise

Nachdem ich in den vorherigen Tutorials zu Processing.py, dem Python-Mode von Processing, schon mit Punkten und Linien hantiert habe, wird es nun Zeit, etwas mit Kreisen und Ellipsen anzustellen (sie werden in Processing mit dem gleichen Befehl erzeugt).

Ein einfacher Kreis ist schnell erzeugt. Mit diesem kleinen Sketch malen Sie einen grellroten Kreis auf schwarzem Grund:

def setup():
    size(500, 500)

def draw():
    background(0)
    fill(255, 0, 0)
    ellipse(width/2, height/2, 450, 450)

Die Funktion ellipse() besitzt vier Parameter, die ersten beiden sind die x- und y-Koordinaten, die per Default die Mitte des Kreises oder der Ellipse bezeichnen, die beiden anderen sind der Durchmesser des Kreises oder der Ellipse (auch wenn sie in der Literatur oft mit r bezeichnet werden, nicht der Radius). Bei einem Kreis müssen die letzten beiden Parameter immer den gleichen Wert besitzen. Wenn Sie aber zum Beispiel die Funktion mit

    ellipse(width/2, height/2, 350, 450)

oder

    ellipse(width/2, height/2, 450, 350)

aufrufen, dann sehen Sie, wie aus den Kreisen Ellipsen werden.

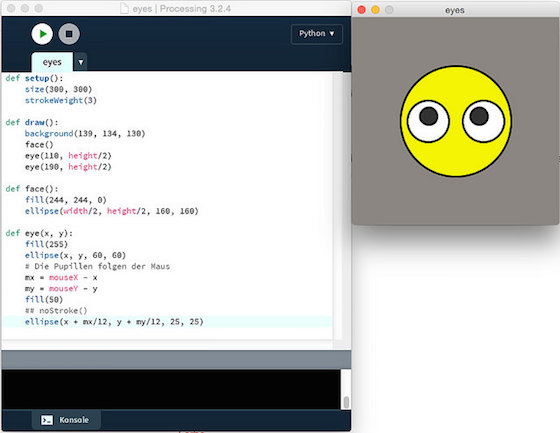
Nun steht Processing aber für Interaktivität. Daher möchte ich aus fünf Kreisen ein Gesicht zaubern, dessen Pupillen dem Mauszeiger folgen. Auch dieser Sketch ist hübsch kurz geraten:

def setup():
    size(300, 300)
    strokeWeight(3)

def draw():
    background(139, 134, 130)
    face()
    eye(110, height/2)
    eye(190, height/2)

def face():
    fill(244, 244, 0)
    ellipse(width/2, height/2, 160, 160)

def eye(x, y):
    fill(255)
    ellipse(x, y, 60, 60)
    # Die Pupillen folgen der Maus
    mx = mouseX - x
    my = mouseY - y
    fill(50)
    ellipse(x + mx/12, y + my/12, 25, 25)

Es wäre nicht wirklich notwendig gewesen, aber der Modularität willen habe ich das Zeichnen des Gesichtes in die Funktion face() und das Zeichnen der Augen in die Funtion eye() ausgelagert. Mit den Werten in dem ellipse()-Aufruf bei den Augen habe ich solange experimentiert, bis sie meinen Vorstellungen entsprachen. Nun sieht aber alles aus wie in dem obigen Screenshot.

Credits

Die Idee zu den Augen habe ich einem (Java-) Processing-Tutorial von Thomas Koberger entnommen, das ich variiert und nach Processing.py übertragen habe. Auf seinen Seiten findet man übrigens noch viele weitere, interessante und lehrreiche Tutorials, so daß ich Ihnen einen Besuch dort empfehle.

Für die Farben habe ich mal wieder wild nach einer Seite mit Farbpaletten gegoogelt und fand die gefundene dann zwar nicht unbedingt schön, aber ungemein praktisch.

Spaß mit Kreisen: Konfetti

Der folgende kleine Sketch ist nicht mehr als eine Fingerübung. Er soll Ihnen zeigen, wie man schon mit wenigen Zeilen Code und Processings-Zufallsfunktion random() viele bunte Konfetti-Schnipsel auf den Bildschirm zaubern kann:

Und hier der Quellcode des Sketches in Processing.py:

def setup():
    size(400, 400)
    frame.setTitle("Konfetti!")
    background(0)

def draw():
    x = random(width)
    y = random(height)
    dia = random(5, 25)
    r = random(255)
    g = random(255)
    b = random(255)
    fill(r, g, b)
    ellipse(x, y, dia, dia)

Für so wenige Programmzeilen ist das Ergebnis doch recht ansprechend, oder?

Syntaktischer Zucker: »with« in Processing.py

Wenn man in Processing.py irgendetwas zum Beispiel zwischen beginShape() und endShape() klammert, fühlt sich das nicht sehr »pythonisch« an. Ich denke dann die ganze Zeit: Das gehört doch eingerückt! In Processings Java-Mode kann man das auch machen, weil man in Java Leerzeichen einsetzen kann, wie man will – sie haben dort keine Bedeutung. Doch Python reagiert ja sehr sensibel auf Einrückungen, da hier Leerzeichen Teil der Syntax sind. Aber die Macher von Processing.py haben dies bedacht und uns einen Ausweg aus diesem Dilemma geboten: Das with-Statement.

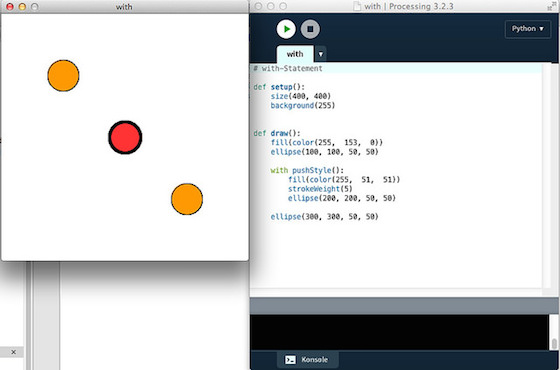
In seiner einfachsten Form sieht das so aus. Statt zum Beispiel

def setup():
    size(400, 400)
    background(255)

def draw():
    fill(color(255,  153,  0))
    strokeWeight(1)
    ellipse(100, 100, 50, 50)
    fill(color(255,  51,  51))
    strokeWeight(5)
    ellipse(200, 200, 50, 50)
    fill(color(255,  153,  0))
    strokeWeight(1)
    ellipse(300, 300, 50, 50)

zu schreiben, schreibt man einfach:

def setup():
    size(400, 400)
    background(255)


def draw():
    fill(color(255,  153,  0))
    ellipse(100, 100, 50, 50)

    with pushStyle():
        fill(color(255,  51,  51))
        strokeWeight(5)
        ellipse(200, 200, 50, 50)
    ellipse(300, 300, 50, 50)

Die Ausgabe ist in beiden Fällen identisch, aber der zweite Sketch ist in meinen Augen bedeutend eleganter und fühlt sich viel pythonischer an. Außerdem erspart man sich viel Tipparbeit.

Da ich die Verwendung des with-Statements auch erst durch eines der mitgelieferten Beispielprogramme herausbekommen habe, hier eine (hoffentlich) komplette Liste der Möglichkeiten:

    with pushMatrix():          pushMatrix()
        translate(10, 10)       translate(10, 10)
        rotate(PI/3)            rotate(PI/3)
        rect(0, 0, 10, 10)      rect(0, 0, 10, 10)
    rect(0, 0, 10, 10)          popMatrix()
                                rect(0, 0, 10, 10)

with beginContour():             beginContour()
    doSomething()                doSomething()
                                 endContour()


with beginCamera():              beginCamera()
    doSomething()                doSomething()
                                 endCamera()

with beginPGL():                 beginPGL()
    doSomething()                doSomething()
                                 endPGL()

with beginShape():               beginShape()
    vertex(x, y)                 vertex(x, y)
    vertex(j, k)                 vertex(j,k)
                                 endShape()


with beginShape(TRIANGLES):      beginShape(TRIANGLES)
    vertex(x, y)                 vertex(x, y)
    vertex(j, k)                 vertex(x, y)
                                 endShape()

with beginClosedShape():         beginShape()
    vertex(x, y)                 vertex(x, y)
    vertex(j, k)                 vertex(j, k)
                                 endShape(CLOSED)

Links steht die Schreibweise mit dem with()-Statement, rechts die traditionelle Form. Abgesehen davon, daß die with-Schreibweise immer mindestens eine Zeile kürzer ist, sorgt sie durch die Einrückungen auch für eine bessere Übersicht und eine bessere Lesbarkeit.

Spaß mit Kreisen (2) in Processing.py: Cantor-Käse und mehr

Wie im letzten Beitrag gezeigt, ist es in Processing recht einfach, einfache Kreise oder Ellipsen zu zeichnen. Aber das ist auf die Dauer natürlich ein wenig langweilig, daher wende ich mich nun einer rekursiven Figur zu, die zwar ebenfalls nur aus Kreisen besteht, aber dennoch einige interessante Eigenschaften aufweist, dem Cantor-Käse, einer Figur, die der Cantor-Menge topologisch ähnlich ist. Sie wird konstruiert, in dem aus einem Kreis bis auf zwei kleinere Kreise alles entfernt wird. Aus diesen zwei kleineren Kreisen wird wiederum bis auf zwei kleinere Kreise alles entfernt. Nun hat man schon vier Kreise, aus denen man jeweils bis auf zwei kleinere Kreise alles entfernt. Und so weiter und so fort …

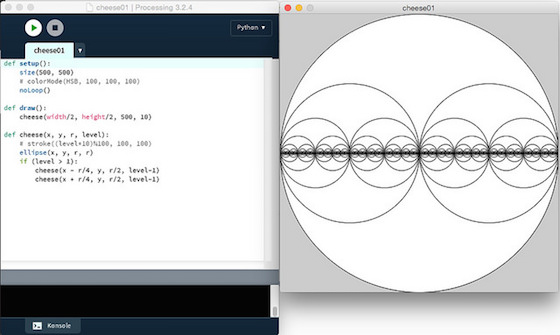
Das schreit natürlich nach einer rekursiven Funktion und die ist in Python recht schnell erstellt:

def setup():
    size(500, 500)
    # colorMode(HSB, 100, 100, 100)
    noLoop()

def draw():
    cheese(width/2, height/2, 500, 10)

def cheese(x, y, r, level):
    ellipse(x, y, r, r)
    if (level > 1):
        cheese(x - r/4, y, r/2, level-1)
        cheese(x + r/4, y, r/2, level-1)

Das Ergebnis können Sie in obenstehendem Screenshot bewundern. Im Screenshot sieht man noch, daß ich auch versucht habe, mit Farbe zu experimentieren, aber ein wirklich befriedigendes Ergebnis war dabei nicht herausgekommen

Ich hatte diese Figur auch schon mal in Shoes zeichnen lassen und dabei Porbleme mit der Rekursiontiefe festgestellt (ab einer Rekursionstiefe von 15 stürzte Shoes gnadenlos ab). Hier scheint Processing robuster zu sein, eine Rekursionstiefe von 15 nahm die Software gelassen hin, ließ sich dann natürlich Zeit mit der Ausgabe. Das muß schließlich alles berechnet werden.

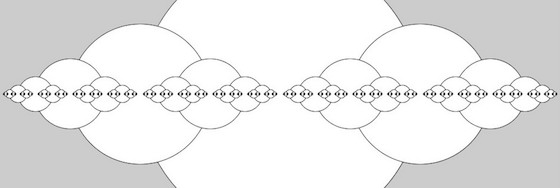
Weil der Durchmesser der Kreise in der Literatur oft mit r bezeichnet wird, neige ich dazu, Radius und Durchmesser zu verwechseln. Setzt man dann den Algorithmus 1:1 um, zum Beispiel wie in diesem Sketch

def setup():
    size(1000, 500)
    noLoop()

def draw():
    cheese(width/2, height/2, 500, 10)

def cheese(x, y, r, level):
    ellipse(x, y, r, r)
    if (level > 1):
        cheese(x - r/2, y, r/2, level-1)
        cheese(x + r/2, y, r/2, level-1)

kommt die Figur heraus, die den Kopf dieses Beitrages ziert. Das ist zwar streng genommen kein Cantor-Käse mehr, aber dennoch ein interessantes Ergebnis. Das macht den Vorteil des schnellen Skizzierens in Processing aus: Selbst Fehler können unerwartete und notierenswerte Ergebnisse liefern. Man hebt dann den Sketch einfach auf.

Cantors Doppelkäse

Schon bei meinen Experimenten mit Shoes hatte ich mich gefragt, wie es denn aussähe, wenn man diese Figur sich nicht nur in der Horizontalen, sondern auch in der Vertikalen ausbreiten läßt?

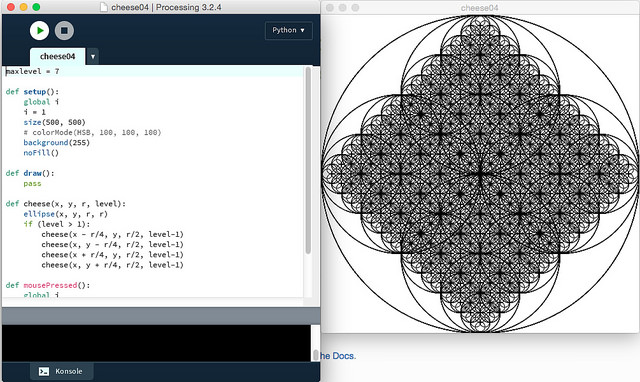
Dabei habe ich auch gleich ein interaktives Element eingeführt: Startet man das Programm, zeigt es zuerst nur ein weißes Fenster, nach dem ersten Mausklick sieht man die erste Rekursionstiefe, einen einfachen Kreis, der nächste Mausklick zeigt vier darin eingeschriebene Kreise, der nächste Mausklick zeigt dann in jedem der kleinen Kreise wiederum vier eingeschriebene Kreise und so weiter und so fort …

maxlevel = 7

def setup():
    global i
    i = 1
    size(500, 500)
    # colorMode(HSB, 100, 100, 100)
    background(255)
    noFill()

def draw():
    pass

def cheese(x, y, r, level):
    ellipse(x, y, r, r)
    if (level > 1):
        cheese(x - r/4, y, r/2, level-1)
        cheese(x, y - r/4, r/2, level-1)
        cheese(x + r/4, y, r/2, level-1)
        cheese(x, y + r/4, r/2, level-1)

def mousePressed():
    global i
    cheese(width/2, height/2, 500, i)
    i += 1
    if (i >= maxlevel):
        noLoop()

Das Programm stoppt dann bei einer Rekursionstiefe von sieben. Auch hier ist Processing robuster als Shoes, höhere Rekursionstiefen waren kein Problem, nur man sah dann nicht viel mehr als ein auf der Spitze stehendes Quadrat mit ein paar Ausbuchtungen – die Auflösung des Bildschirms setzt hier neuem Erkenntnisgewinn Grenzen.

Interessant und neu für mich war, daß man – um überhaupt ein Zeichenfenster zu bekommen, in das man mit der Maus klicken konnte – eine leere draw()-Funktion benötigte. Eigentlich logisch, aber ich hatte vorher nie darüber nachgedacht.

Literatur

• Clifford A. Pickover: Mit den Augen des Computers. Phantastische Welten aus dem Geist der Maschine, München (Markt und Technik) 1992. Diese deutsche Übersetzung von Computers and the Imagination ist eine geniale Fundgrube für alle, die Simulationen und mathematische Spielereien mit dem Computer lieben. Es ist eines der besten Bücher Pickovers. Dem Cantor-Käse ist auf den Seiten 171-181 ein eigenes Kapitel gewidmet.
• Chris Robart: Programming Ideas: For Teaching High School Computer Programming, (PDF 260 KB, 2nd Edition) 2001. Ebenfalls eine Fundgrube voller Ideen, deren Download sich in jedem Fall lohnt.

Weitere geometrische Grundformen

Processing besitzt ein kleines Set von geometrischen Primitiven in 2D (im Englischen Shapes genannt) mit denen sich so einiges anstellen läßt. Neben den schon bekannten Punkten und Kreisen und Ellipsen, gibt es noch einige andere, die ich der Reihe nach vorstellen möchte:

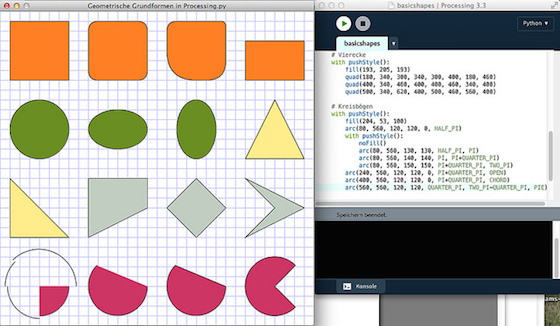
Rechtecke

Rechtecke (rect()) sind die einfachste Grundform. Dennoch besitzen auch sie einige Besonderheiten. Es gibt sie nämlich in der Form

rect(x, y, w, h)
rect(x, y, w, h, r)
rect(x, y, w, h, tl, tr, br, bl)

Bei vier Parametern sind die ersten beiden Parameter, die x- und y-Koordinate der linken, oberen Ecke des Rechtecks und die beiden anderen Parameter geben die Breite und Höhe des Rechtecks an. Gilt w == h, dann ist das Rechteck natürlich ein Quadrat.

Wird rect() mit fünf Parametern aufgerufen, dann ist der fünfte Parameter als Radius für die Abrundung der Ecken verantwortlich. Mit acht Paramtern bekommt jede Ecke einen eigenen Radius für die abgerundeten Ecken einen eigenen Radius zugeschrieben. Dabei wird von links oben über rechts oben und rechts unten nach links unten vorgegangen.

Rechtecke besitzen per Default den rectMode(CORNER). Wird ein anderer rectMode() eingegeben, dann ändert sich die Bedeutung des dritten und vierten Parameters. Ist er CORNERS, dann bennen die ersten beiden Paramter weiterhin die linke, obere Ecke, der dritte und vierte Parameter aber die x- und y-Koordinaten der rechten, unteren Ecke.

Ist der rectMode(CENTER), dann bennen die ersten beiden Parameter den Mittelpunkt des Rechteckes, der dritte und vierte Parameter gibt aber weiterhin die Breite und Höhe des Rechtecks an.

Dahingegen sind beim rectMode(RADIUS) die ersten beiden Paramter die x- und y-Koordinaten des Mittelpunkts des Rechtecks, während die dritte und vierte Koordinate jeweils die Hälfte der Breite und die Hälfte der Höhe angeben.

Der rectMode(CENTER) ist vor allen Dingen dann vom Vorteil, wenn Rechtecke mit Kreisen oder Ellipsen koordiniert werden, da bei diesen per Default ellipseMode(CENTER) gilt. Zu diesen kommen ich daher im Anschluß noch einmal.

Kreise und Ellipsen

Ellipsen und Kreise (als Spezialform der Ellipse) werden in Processing mit dem Befehl

ellipse(x, y, w, h)

erzeugt. Dabei sind x und y der Mittelpunkt der Ellipse und w und h per Default die Breite und Höhe der Ellipse. Sind w == h, dann bildet die Ellipse einen Kreis.

Ändert man jedoch den Default-Mode CENTER, dann ergeben sich folgende Bedeutungsänderungen der vier Parameter.

Beim ellipseMode(RADIUS) bilden die ersten beiden Parameter weiterhin den Mittelpunkt der Ellipse oder des Kreises, der dritte und vierte Parameter gibt jedoch die Hälfte der Höhe und die Hälfte der Breite der Ellipse oder des Kreises an.

Ist der ellipseMode(CORNER), dann benennen die x- und y-Koordinaten die linke, obere Ecke der Ellipse oder des Kreises, die beiden anderen Parameter geben weiterhin die Breite und Höhe an.

Heißt es jedoch ellipseMode(CORNERS), dann bennenen die x- und y-Koordinaten die linke, obere Ecke des die Ellipse oder den Kreis umschließenden Rechtecks, der dritte und vierte Parameter die rechte untere Ecke dieses Rechtecks.

Die Modes CORNER, CORNERS, CENTER und RADIUS müssen immer in Großbuchstaben eingegeben werden, da Processing und Python streng zwischen Groß- und Kleinschreibung unterscheiden.

Dreieck

Das Dreieick ist eines der einfachsten geometrischen Grundformen in Processing. Es existiert nur in der Form

triangle(x1, y1, x2, y2, x3, y3)

und hat auch keinen besonderen Mode. Die jeweiligen x- und y-Koordinagen sind die Koordinaten des ersten, zweiten und dritten Punktes. Bei der Reihenfolge wird – oben beginnend – immer im Uhrzeigersinn vorgegangen. Das ist alles.

Unregelmäßige Vierecke

Ähnlich einfach verhält es sich mit den unregelmäßigen Vierecken. Sie werden mit

quad(x1, y1, x2, y2, x3, y3, x4, y4)

erzeugt und auch hier sind es absolute Koordinaten und das Gebilde besitzt ebenfalls keinen besonderen Mode. Auch hier wird bei der Zählung links oben begonnen und dann werden die Ecken ebenfalls im Uhrzeigersinn abgearbeitet.

Kreisbögen

Kreisbögen sind mit der Ellipse (genauer: dem Kreis verwandt) und besitzen die gleichen Modi wie diese (mit dem gleichen Default CENTER). Sie werden wie folgt aufgerufen:

arc(x, y, w, h, start, stop)
arc(x, y, w, h, start, stop, mode)

Die x- und y-Koordinaten sind im Default-Mode der Mittelpunkt des Kreises, während w und h im Default-Mode die Breite und Höhe des Kreisen angeben. start und stop sind die Winkel (in radians) für die Länge des Kreisbogens.

Dann gibt es hier noch einen besonderen mode. Der kann OPEN (das ist der Default), CHORD oder PIE heißen. Im Default OPEN bleibt der Kreisbogen offen, falls es jedoch ein fill() gibt, wird er dennoch gefüllt. Bei CHORD wird der Kreisbogen geschlossen und bei PIE bildet er ein Kuchenstück, wie man es von Tortengraphiken kennt.

Der Quelltext

In diesem Beispielprogramm habe ich alle angesprochenen geometrischen Primitive in ihren diversen Erscheinungsformen zeichnen lassen. Mit dem oben geschriebenen dürfte es einfach nachzuvollziehen ein.

def setup():
    size(640, 640)
    frame.setTitle("Geometrische Grundformen in Processing.py")
    # noLoop()

def draw():
    background(255)
    drawGrid()
    stroke(0)

    # Rechtecke
    with pushStyle():
        fill(255,127,36)
        rect(20, 20, 120, 120)
        rect(180, 20, 120, 120, 20)
        rect(340, 20, 120, 120, 20, 10, 40, 80)
        rect(500, 60, 120, 80)

    # Kreise und Ellipsen
    with pushStyle():
        fill(107, 142, 35)
        ellipse(80, 240, 120, 120)
        ellipse(240, 240, 120, 80)
        ellipse(400, 240, 80, 120)

    # Dreiecke
    with pushStyle():
        fill(255, 236, 139)
        triangle(560, 180, 620, 300, 500, 300)
        triangle(20, 340, 140, 460, 20, 460)

    # Vierecke
    with pushStyle():
        fill(193, 205, 193)
        quad(180, 340, 300, 340, 300, 400, 180, 460)
        quad(400, 340, 460, 400, 400, 460, 340, 400)
        quad(500, 340, 620, 400, 500, 460, 560, 400)

    # Kreisbögen
    with pushStyle():
        fill(204, 53, 100)
        arc(80, 560, 120, 120, 0, HALF_PI)
        with pushStyle():
            noFill()
            arc(80, 560, 130, 130, HALF_PI, PI)
            arc(80, 560, 140, 140, PI, PI+QUARTER_PI)
            arc(80, 560, 150, 150, PI+QUARTER_PI, TWO_PI)
        arc(240, 560, 120, 120, 0, PI+QUARTER_PI, OPEN)
        arc(400, 560, 120, 120, 0, PI+QUARTER_PI, CHORD)
        arc(560, 560, 120, 120, QUARTER_PI, TWO_PI-QUARTER_PI, PIE)


def drawGrid():
    stroke(200, 200, 255)
    for i in range(0, width, 20):
        line(i, 0, i, height)
    for i in range(0, height, 20):
        line(0, i, width, i)

Ich habe das Fenster mit einem 20 x 20 Pixel großen Raster wie auf kariertem Schulpapier versehen, damit Sie die Eckpunkte der einzelnen Shapes auszählen können, falls Ihnen die Koordinaten nicht sofort klar werden.

Credits

Teilweise folgt dieser Sketch einer Idee von Jan Vantomme aus seinem Buch »Processing 2: Creative Coding Programming Cookbook« (Seiten 31 ff.). Ich habe sie abgewandelt, die Beispiele für die Kreisbögen hinzugefügt und vom Java-Mode in den Python-Mode übertragen.

Ein kleines Planetensystem

Als nächstes Projekt möchte ich eine kleine Animation eines Planetensystems aus Kreisen und Rechtecken entwickeln. Ich weiß, Planeten sind meist kugelförmig und keine Kisten, aber in der virtuellen Welt von Processing ist alles möglich. Außerdem möchte ich damit zeigen, wie nützlich die Transformationsoperatoren translate() und rotate() sein können und dafür brauche ich die Rechtecke zur Verdeutlichung.

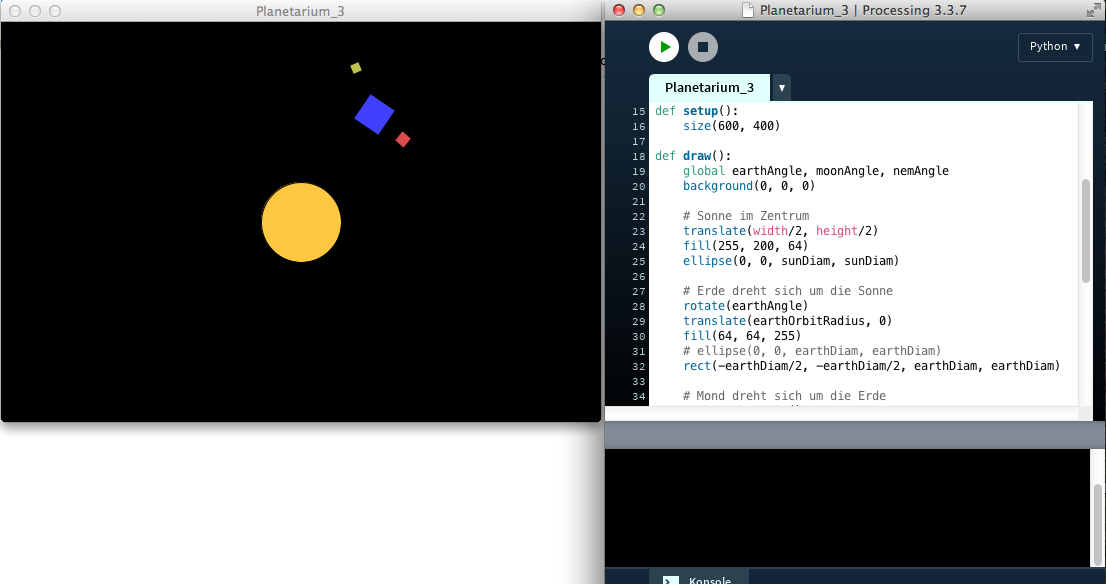
Ich beginne mit einem einfachem System eines Planeten, der seinen Fixstern umkreist, und dieser besitzt einen Trabanten, der wiederum den Planeten umreist. Der Einfachheit halber habe ich die Akteure Sonne, Erde und Mond genannt.

Zu Beginn des Sketches lege ich erst einmal ein paar Zahlen fest:

sunDiam = 80

earthDiam = 30
earthOrbitRadius = 130
earthAngle = 0

moonDiam = 10
moonOrbitRadius = 50
moonAngle = 0

Diese Zahlen sind durch keine physikalische Wirklichkeit gedeckt, sondern einfach so lange durch Experimente herausgesucht worden, bis sich eine ansprechende Animation ergab.

Die setup()-Funktion legt einfach nur die Größe des Ausgabefensters fest:

def setup():
    size(600, 400)

In draw() setze ich den Hintergrund auf schwarz und dann zeichne ich die Sonne in die Mitte des Ausgabefensters:

def draw():
    global earthAngle, moonAngle
    background(0, 0, 0)

    # Sonne im Zentrum
    translate(width/2, height/2)
    fill(255, 200, 64)
    ellipse(0, 0, sunDiam, sunDiam)

Die Zeile translate(width/2, height/2) sorgt dafür, daß der Nullpunkt des Koordinatensystem vom linken oberen Rand in die Mitte des Ausgabefensters gelegt wird und so die Sonne mit ellipse(0, 0, sunDiam, sunDiam) auch genau dort gezeichnet wird. Probiert es aus, der Sketch ist so lauffähig.

Die beiden Variablen earthAngle und moonAngle sind die beiden einzigen Variablen, die sich später in der draw()-Funktion noch ändern werden, daher mußten sie als global definiert werden.

Nun zur Erde, die die Sonne umkreist:

    # Erde dreht sich um die Sonne
    rotate(earthAngle)
    translate(earthOrbitRadius, 0)
    fill(64, 64, 255)
    ellipse(0, 0, earthDiam, earthDiam)

    earthAngle += 0.01

Wenn Sie diese Zeilen Code in die draw()-Funktion unterhalb der Sonne einfügen, bekommen Sie eine blaue Erde, die sich langsam um die Sonne bewegt. Denn mit translate(earthOrbitRadius, 0) wurde das Koordinatensystem erneut verschoben, 180 Pixel von der Sonne entfernt aber auf der gleichen y-Achse wie das Koordinatensystem der Sonne. Da rotate() vor der Koordinatentransformation aufgerufen wird, dreht sich die Erde noch um die Sonne und das Koordinatensystem der Sonne rotiert, ein rotate() hinter der Koordinatentransformation würde bewirken, daß sich die Erde um sich selbst dreht – das heißt, daß das Koordinatensystem der Erde rotieren würde.

Zum Schluß wird noch der Mond angehängt:

    # Mond dreht sich um die Erde
    rotate(moonAngle)
    translate(moonOrbitRadius, 0)
    fill(192, 192, 80)
    ellipse(0, 0, moonDiam, moonDiam)

    moonAngle += 0.01

Durch diese Koordinatentransformation steht der Mond im gleichen Verhältnis zur Erde wie die Erde zur Sonne, der Ursprung des Koordinatensystems liegt nun 50 Pixel vom Erdmittelpunkt entfernt. Natürlich rotiert in diesen Zeilen das Koordinatensystem der Erde, damit der Eindruck entsteht, daß der Mond um die Erde Kreist.

Das alles funktioniert natürlich nur, weil bei jedem erneuten Durchlauf der draw()-Funktion das Koordinatensystem zurückgesetzt wird, also alle Transformationen »vergessen« werden.

Nun kann man bei Kreisen schwer erkennen, ob sie wirklich rotieren, daher habe ich in einer zweiten Fassung, Sie Kreise von Erde und Mond durch Quadrate ersetzt (ich habe – damit Ihr die Position der Codezeilen finden, die ersetzte Kreisfunktion jeweils auskommentiert stehen lassen, die Rechteckfunktion wird jeweils direkt unter der auskommentierten Zeile eingefügt):

    # ellipse(0, 0, earthDiam, earthDiam)
    rect(-earthDiam/2, -earthDiam/2, earthDiam, earthDiam)
    …
    # ellipse(0, 0, moonDiam, moonDiam)
    rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)

Wenn Sie das Programm jetzt starten, dreht sich eine große blaue Kiste um die Sonne mit einer kleinen grauen Kiste, die sich um die Erde dreht und Sie können die Rotation der beiden Kisten genau beobachten.

Doch was ist, wenn ein zweiter Mond – nennen wir ihn Nemesis – um die Erde kreisen soll? Das Koordinantensystem der Erde ist ja schon vom Koordinatensystem des Mondes ersetzt worden. Sie brauchen also eine Funktion, die das Koordinatensystem nur temporär verschiebt, so daß man auf das alte Koordinatensystem wieder zrückgreifen kann, wenn es benötigt wird. Genau dafür gibt es in Processing das Funktionenpaar pushMatrix() und popMatrix(). Mit pushMatrix() wird das bisherige Koordinatensystem auf einen Stack gelegt und mit popMatrix() wird es wieder zurückgeholt. Und in Processing.py gibt es noch, wie ich weiter oben gezeigt hatte, eine besondere Möglichkeit, nämlich das width-Statement, die das jeweilige popMatrix() überflüssig macht: Solange der Code unter dem with-Statement eingerückt ist, wird mit den neuen Koordinaten des width-Statements gearbeitet, wird der Code wieder ausgerückt, werden die auf den Stack gelegten Koordinaten zurückgeholt.

Erst einmal braucht natürlich Nemesis seinen eigenen Satz Variablen,

nemDiam = 12
nemOrbitRadius = 38
nemAngle = 0

wobei nemAngle analog zu den anderen Winkeln zu Beginn der draw()-Schleife als global definiert werden muß:

    global earthAngle, moonAngle, nemAngle

Und dann habe ich Nemesis und dem Mond jeweils eine eigene (Koordinaten-) Matrix spendiert

    # Mond dreht sich um die Erde
    with pushMatrix():
        rotate(moonAngle)
        translate(moonOrbitRadius, 0)
        fill(192, 192, 80)
        # ellipse(0, 0, moonDiam, moonDiam)
        rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)

    # Nemesis dreht sich um die Erde
    with pushMatrix():
        rotate(nemAngle)
        translate(nemOrbitRadius, 0)
        fill(220, 75, 75)
        # ellipse(0, 0, nemDiam, nemDiam)
        rect(-nemDiam/2, -nemDiam/2, nemDiam, nemDiam)

und zum Schluß nemAngle um 0.015 inkrementiert. Das gesamte Programm sieht nun so aus:

sunDiam = 80

earthDiam = 30
earthOrbitRadius = 130
earthAngle = 0

moonDiam = 10
moonOrbitRadius = 50
moonAngle = 0

nemDiam = 12
nemOrbitRadius = 38
nemAngle = 0

def setup():
    size(600, 400)

def draw():
    global earthAngle, moonAngle, nemAngle
    background(0, 0, 0)

    # Sonne im Zentrum
    translate(width/2, height/2)
    fill(255, 200, 64)
    ellipse(0, 0, sunDiam, sunDiam)

    # Erde dreht sich um die Sonne
    rotate(earthAngle)
    translate(earthOrbitRadius, 0)
    fill(64, 64, 255)
    # ellipse(0, 0, earthDiam, earthDiam)
    rect(-earthDiam/2, -earthDiam/2, earthDiam, earthDiam)

    # Mond dreht sich um die Erde
    with pushMatrix():
        rotate(moonAngle)
        translate(moonOrbitRadius, 0)
        fill(192, 192, 80)
        # ellipse(0, 0, moonDiam, moonDiam)
        rect(-moonDiam/2, -moonDiam/2, moonDiam, moonDiam)

    # Nemesis dreht sich um die Erde
    with pushMatrix():
        rotate(nemAngle)
        translate(nemOrbitRadius, 0)
        fill(220, 75, 75)
        # ellipse(0, 0, nemDiam, nemDiam)
        rect(-nemDiam/2, -nemDiam/2, nemDiam, nemDiam)

    earthAngle += 0.01
    moonAngle += 0.01
    nemAngle += 0.015

Natürlich hätte man die Nemesis betreffenden Zeilen nicht in eine eigenes width-Statement klammern müssen, aber so ist es auberer und Sie können der Erde noch einen dritten und einen vierten Trabanten spendieren, ohne mit den Koordinatensystemen durcheinander zu kommen.

Wenn Sie das Programm laufen lasen, werden Sie sehen, warum ich für die Erde und ihre Trabanten Rechtecke gewählt habe. So ist zu erkennen, daß die Erde mit genau einer Seite immer zur Sonne zeigt und die beiden Trabanten ebenfalls mit genau einer Seite zur Erde. Das ist, weil sie sich jeweils in ihrem eigenen Koordinatensystem bewegen, dessen eine Achse immer das Zentrum des darüberliegenden Koordinatensystems schneidet.

Für die Monde ist das okay, wenn Sie der Erde aber Tag und Nacht spendieren wollen, müssen Sie ihr noch ein zweites rotate() nach der Koordinatentransformation spendieren.

Natürlich ist das Progrämmchen ausbaubar. Sie können zum Beispiel mehrere Planeten jeweils mit ihren eigenen Koordinatensystemen um den Fixstern kreisen lassen. Alle diese Planeten können Sie mit Monden umgeben, die wiederum ihr eigenes Koordinatensystem besitzen. Und wenn Sie wirkliche Helden sein wollen: Schnappt Sie sich ein Buch mit den Keplerschen Gesetzen zur Planetenbewegung und simulieren damit ein realistischeres Planetensystem.

Literatur

Die Idee zu diesem Sketch und einige der Parameter habe ich dem wunderbaren Buch »Processing for Visual Artists – How to Create Expressive Images and Interactive Art« von Andrew Glassner (Natick, MA, 2010), Seiten 192-200 entnommen und von Java nach Python portiert.

Eine analoge Uhr aus Kreisbögen

In seiner 74. Coding-Challenge auf YouTube zeigte Daniel Shiffman, wie man mit P5.js, dem JavaScript-Mode von Processing, eine analoge Uhr aus Kreisbögen programmiert. Inspiriert wurde er von John Maedas 12 o'Clocks-Projekt und ich unterlag der Versuchung, Shiffmans JavaScript-Programm nach Processing.py zu portieren:

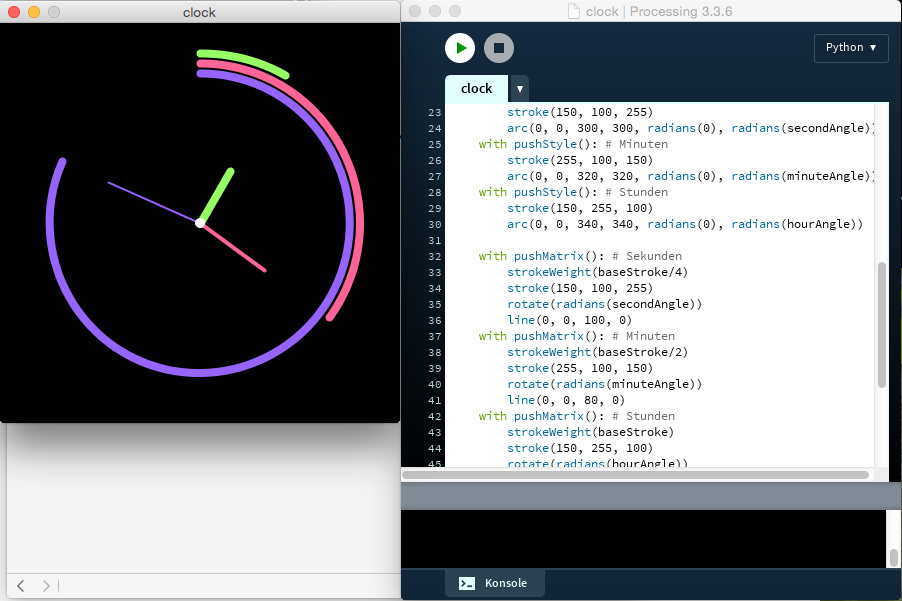
Dabei habe ich gegenüber dem Original-Script nur einige kleine Veränderungen vorgenommen.Ich habe die Stunden in den äußeren Kreisbogen gelegt und dadurch die Sekunden in den inneren Kreisbogen. Und ich habe die Zeiger der Uhr nicht nur in unterschiedlichen Längen, sondern auch in unterschiedliche Dicken zeichnen lassen, wie man es von analogen Uhren gewohnt ist. Außertdem habe ich heftigen Gebrauch vom with-Statement gemacht, das in Processing.py in vielen Fällen nicht nur das push und pop ersetzen, sondern auch ungterschiedliche Statii klammern kann.

Der Quellcode

Meiner Meinung nach ist der Quellcode gegenüber der JavaScript-Version übersichtlicher geworden und leichter zu durchschauen. Das liegt aber sicher nicht an meinen genialen Programmierkenntnissen (die sind eher bescheiden), sondern ist der Klarheit von Python geschuldet:

baseStroke = 8

def setup():
    size(400, 400)
    frameRate(30)

def draw():
    background(0)
    translate(width/2, height/2)
    rotate(radians(-90))

    hr = hour()
    mn = minute()
    sc = second()

    secondAngle = map(sc, 0, 60, 0, 360)
    minuteAngle = map(mn, 0, 60, 0, 360)
    hourAngle = map(hr%12, 0, 12, 0, 360)
    noFill()
    strokeWeight(baseStroke)

    # Kreisbögen
    with pushStyle(): # Sekunden
        stroke(150, 100, 255)
        arc(0, 0, 300, 300, radians(0), radians(secondAngle))
    with pushStyle(): # Minuten
        stroke(255, 100, 150)
        arc(0, 0, 320, 320, radians(0), radians(minuteAngle))
    with pushStyle(): # Stunden
        stroke(150, 255, 100)
        arc(0, 0, 340, 340, radians(0), radians(hourAngle))

    # Zeiger
    with pushMatrix(): # Sekunden
        strokeWeight(baseStroke/4)
        stroke(150, 100, 255)
        rotate(radians(secondAngle))
        line(0, 0, 100, 0)
    with pushMatrix(): # Minuten
        strokeWeight(baseStroke/2)
        stroke(255, 100, 150)
        rotate(radians(minuteAngle))
        line(0, 0, 80, 0)
    with pushMatrix(): # Stunden
        strokeWeight(baseStroke)
        stroke(150, 255, 100)
        rotate(radians(hourAngle))
        line(0, 0, 60, 0)

    noStroke()
    fill(255, 255, 255)
    ellipse(0, 0, 10, 10)

Links

• Golan Levins Notizen zu Maedas 12 o’Clocks nebst Anhang
• Alca's Clock Collection auf CodePen

Visualisierung: Die Sonntagsfrage

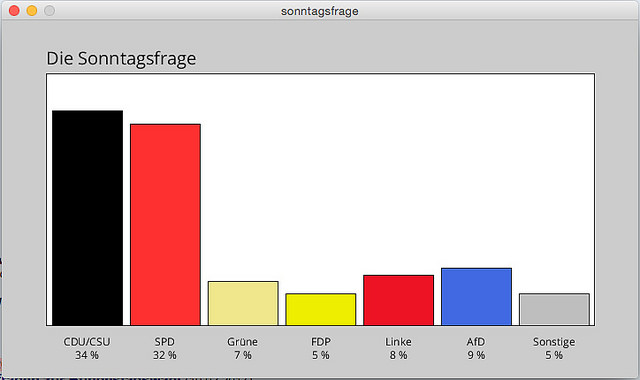
Man kann sich durchaus zu Recht fragen, ob es überhaupt sinnvoll ist, so etwas wie den obigen Barchart in Processing.py per Fuß zu erstellen. Schließlich gibt es (auch in Python) Bibliotheken wie etwa die Matplotlib, die für diese Aufgabe spezialisiert sind und mit wenigen Zeilen Code wunderbarer Graphiken auf den Monitor zaubern und sie auch gleichzeitig publikationsreif in einer Datei ablegen können.

Aber auf der anderen Seite schadet es nichts, wenn man selber genau weiß, wie man so etwas anstellen kann. Denn zum einem hat man vielleicht Gründe, die Umgebung von Processing.py nicht verlassen zu wollen. Und zum anderen gibt es doch auch immer wieder Spezialfälle, die von den spezialisierten Bibliotheken nicht abgedeckt werden.

Daher habe ich hier einmal die Ergebnisse der Sonntagsfrage (»Wenn am nächsten Sonntag Bundestagswahl wäre …«), die die Forschungsgruppe Wahlen regelmäßig veröffentlicht, nur mit den Hausmitteln von Processing.py in einem einfachen Barchart dargestellt.

Für die Daten, Namen und Farben habe ich drei Listen erstellt. Das hat den Vorteil, daß man bei einer neuen Umfrage nur die Ergebnisse in der Liste prozente[] ändern muß – an den anderen Listen ändert sich zumindest bis zur Bundestagswahl im nächsten Jahr nichts.

Normalerweise werden Rechtecke in Processing ja mit dem Befehl rect(x, y, w, h) erzeugt, setzt man jedoch rectMode(CORNERS), dann werden die realen Eckpunkte als Parameter erwartet, also rect(x1, y1, x2, y2).

Für die Anpassung der Balken an den Bildschirmausschnitt habe ich auf Processings map(value, dataMin, dataMax, targetMin, targetMax)-Funktion zurückgegriffen, die einen Datenwert von einem Bereich in einen anderen überträgt. Nun hat Python selber aber auch noch eine eingebaute map(function, iterable, …)-Funktion, die mit der Processing-Funktion in Konflikt steht. Aber die Macher von Processing.py haben sich viel Mühe gegeben, diesen Konflikt aufzulösen. Erfüllt map() die Signatur der Python-Funktion, wird diese aufgerufen, ansonsten die Processing-Funktion.

Der Quellcode

parteien = ["CDU/CSU", "SPD", u"Grüne", "FDP", "Linke", "AfD", "Sonstige"]
prozente = [34, 32, 7, 5, 8, 9, 5]
farben = [color(0, 0, 0), color(255, 48, 48), color(240, 230, 140),
          color(238, 238, 0), color(238, 18, 37),
          color(65, 105, 225), color(190, 190, 190)]

titel = "Die Sonntagsfrage"

def setup():
    global X1, X2, Y1, Y2
    size(720, 405)
    X1 = 50
    X2 = width - X1
    Y1 = 60
    Y2 = height - Y1
    font1 = createFont("OpenSans-Regular.ttf", 20)
    textFont(font1)
    noLoop()

def draw():
    global X1, X2, Y1, Y2
    fill(255)
    rectMode(CORNERS)
    rect(X1, Y1, X2, Y2)
    fill(0)
    textSize(20)
    text(titel, X1, Y1 - 10)
    delta = (X2 - X1)/(len(prozente))
    w = delta*0.9
    x = w*1.22
    textSize(12)
    for i in range(len(prozente)):
        # Balken zeichnen
        h = map(prozente[i], 0, 40, Y2, Y1)
        fill(farben[i])
        rect(x - w/2, h, x + w/2, Y2)
        # Parteinamen und Prozente unter der X-Achse
        textAlign(CENTER, TOP)
        fill(0)
        text(parteien[i], x, Y2 + 10)
        text(str(prozente[i]) + " %", x, Y2 + 25)
        x += delta

Ansonsten ist der Quellcode leicht nachzuvollziehen. Die Abstands- und Längenwerte für w und delta habe ich durch Experimentieren herausgefunden, ebenso die Startposition von x.

Quellen

Die Zahlen der Forschungsgruppe Wahlen habe ich auf der Seite wahlrecht.de entnommen, dort sind viele weitere Umfrageergebnisse zu Bundes- und Landtagswahlen zu finden. Und den verwendeten Font Open Sans habe ich bei Google Fonts gefunden. Er steht unter der Apache-Lizenz, Version 2. Sie sollten nicht vergessen, die entsprechende Datei OpenSans-Regular.ttf in den data-Folder Ihres Sketches zu schieben, damit Processing.py den Font auch finden kann.

Rosetten-Kurven

In seiner 55. Code-Challenge ließ Daniel Shiffman munter Rosetten-Kurven in P5.js, dem JavaScript-Mode von Processing, zeichnen. Das Video hatte mir keine Ruhe gelassen. Ich wollte so etwas auch unbedingt in Processing.py implementieren.

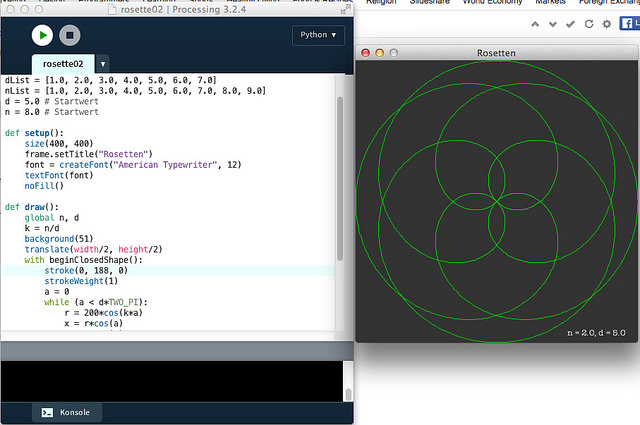
Der Anfang war einfach. Ich bin stur Daniel Shiffman gefolgt und hatte innerhalb kürzester Zeit seinen Code in einen Python-Code verwandelt:

d = 8.0
n = 5.0

def setup():
    size(400, 400)
    frame.setTitle("Rosetten")
    noFill()

def draw():
    k = n/d
    background(51)
    translate(width/2, height/2)
    with beginClosedShape():
        stroke(255)
        strokeWeight(1)
        a = 0
        while (a < d*TWO_PI):
            r = 200*cos(k*a)
            x = r*cos(a)
            y = r*sin(a)
            vertex(x, y)
            a += 0.02

Die einzigen Änderungen sind einmal, daß ich das with-Statement ausgenutzt und daß ich statt der for-Schleife eine while-Schleife verwendet habe, da in Pythons for-Schleifen das Inkrement oder Dekrement ganzzahlig sein müssen.

Doch bin ich zwar durchaus ein Freund des Sketchens, aber jedesmal, wenn ich eine andere Rosette haben will, den Quelltext zu ändern, war dann doch nicht mein Ding. Daher habe ich dann die d- und n- Werte, wie sie in dem oben und im Literaturverzeichnis verlinkten Wikipedia-Artikel genannt sind, in eine Liste gepackt

dList = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0]
nList = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]

und aus dieser Liste dann bei jedem Mausklick zufällig je einen Wert für d und n auswählen lassen:

def mousePressed():
    global n, d
    n = r.choice(nList)
    d = r.choice(dList)

Pythons Random-Bibliothek stellt dafür dankenswerterweise den Befehl choice() zur Verfügung, der diese Listenmanipulation sehr einfach macht.

Der Rest war dann nur noch Kosmetik: In nostalgischer Erinnerung an meine frühen Computerjahre habe ich die Kurve in Grün zeichnen und damit ich weiß, welche Werte der Zufallszahlengenerator mir für d und n ausgewählt hat, habe ich diese unten rechts ausgeben lassen.

Der Quelltext

Für die, die diesen Sketch nachprogrammieren wollen, hier nun auch der vollständige Quelltext meines Experiments:

import random as r

font = None
dList = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0]
nList = [1.0, 2.0, 3.0, 4.0, 5.0, 6.0, 7.0, 8.0, 9.0]
d = 5.0 # Startwert
n = 8.0 # Startwert

def setup():
    size(400, 400)
    frame.setTitle("Rosetten")
    font = createFont("American Typewriter", 12)
    textFont(font)
    noFill()

def draw():
    global n, d
    k = n/d
    background(51)
    translate(width/2, height/2)
    with beginClosedShape():
        stroke(0, 188, 0)
        strokeWeight(1)
        a = 0
        while (a < d*TWO_PI):
            r = 200*cos(k*a)
            x = r*cos(a)
            y = r*sin(a)
            vertex(x, y)
            a += 0.02
        text("n = " + str(n) + ", d = " + str(d), 100, 190)

def mousePressed():
    global n, d
    n = r.choice(nList)
    d = r.choice(dList)

Caveat

Als Font für die Textausgabe habe ich mir den Systemfont »American Typewriter« ausgesucht (ich mag ihn einfach). Dieser steht sicher nicht auf allen Betriebssystemen zur Verfügung, Ihr müßt Euch daher gegebenenfalls einen anderen Systemfont aussuchen.

Literatur

• Rosettenkurven in der deutschsprachigen Wikipedia

Der Baum des Pythagoras

Eine weitere Ikone der fraktalen Geometrie ist der Pythagoras-Baum. Er geht zurück auf den niederländischen Ingenieur und späteren Mathematiklehrer Albert E. Bosman (1891–1961). Er entwarf während des 2. Weltkrieges in seiner Freizeit an einem Zeichenbrett, an dem er sonst U-Boot-Pläne zeichnete, geometrische Muster. Seine Graphiken wurden 1957 in dem Buch »Het wondere onderzoekingsveld der vlakke meetkunde« veröffentlicht.

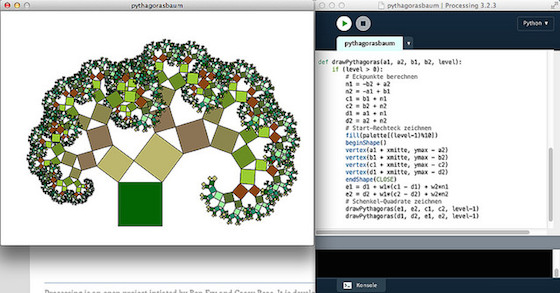
Der Pythagoras-Baum beruht auf einer rekursiven Abbildung des Pythagoras-Lehrsatzes: Die beiden Quadrate auf den Katheten des rechtwinkligen Dreiecks dienen als Verzweigung, auf dem jedes Kathetenquadrat sich wiederum verzweigt.

Die Funktion drawPythagoras

Um die Funktion rekursiv aufrufen zu können, mußte ich sie aus der draw()-Funktion auslagern und sie in einen eigenen Aufruf packen:

def drawPythagoras(a1, a2, b1, b2, level):
    if (level > 0):
        # Eckpunkte berechnen
        n1 = -b2 + a2
        n2 = -a1 + b1
        c1 = b1 + n1
        c2 = b2 + n2
        d1 = a1 + n1
        d2 = a2 + n2
        # Start-Rechteck zeichnen
        fill(palette[(level-1)%10])
        with beginClosedShape():
            vertex(a1 + xmitte, ymax - a2)
            vertex(b1 + xmitte, ymax - b2)
            vertex(c1 + xmitte, ymax - c2)
            vertex(d1 + xmitte, ymax - d2)
        e1 = d1 + w1*(c1 - d1) + w2*n1
        e2 = d2 + w1*(c2 - d2) + w2*n2
        # Schenkel-Quadrate zeichnen
        drawPythagoras(e1, e2, c1, c2, level-1)
        drawPythagoras(d1, d2, e1, e2, level-1)

Zum Zeichnen der einzelnen Quadrate habe ich nicht die rect()-Funktion genutzt, sondern Shapes, mit denen sich Punkte zu einem beliebigen Gebilde oder Polygon zusammefassen lassen. Hierzu müssen sie erst einmal mit with beginClosedShape() geklammert werden. Darin werden dann mit vertex(x, y) nacheinander die einzelnen Punkt aufgerufen, die (im einfachten Fall) durch Linien miteinander verbunden werden sollen. Mit beginClosedShape teile ich dem Sketch auch mit, daß das entstehende Polygon auf jeden Fall geschlossen werden soll, ein einfaches with beginShape() würde es offen lassen.

Der Aufruf ist rekursiv: Nachdem zuerst das Grundquadrat gezeichnet wurde, werden die rechten und die linken Schenkelquadrate gezeichnet, die dann wieder als Grundquadrate für den nächsten Rekursionslevel fungieren.

Processing (und damit auch der Python-Mode von Processing) ist gegenüber Rekursionstiefen realtiv robust. Die benutzte Rekursionstiefe von 12 wird klaglos abgearbeitet, auch Rekursionstiefen bis 20 sind – genügend Geduld vorausgesetzt – kein Problem. Bei einer Rekursionstiefe von 22 verließ mich aber auf meinem betagten MacBook Pro die Geduld.

Die Farben

Für die Farben habe ich eine Palette in einer Liste zusammengestellt, die der Reihe nach die Quadrate einfärbt. Da die Liste nur 10 Elemente enthält, habe ich mit fill(palette[(level-1)%10]) dafür gesorgt, daß nach 10 Leveln die Palette wieder von vorne durchlaufen wird.

Der Quellcode

Da die eigentliche Aufgabe des Programms in die Funktion drawPythagoras() ausgelagert wurde, ist der restlich Quellcode von erfrischender Kürze:

palette = [color(189,183,110), color(0,100,0), color(34,139,105),
           color(152,251,152), color(85,107,47), color(139,69,19),
           color(154,205,50), color(107,142,35), color(139,134,78),
           color(139, 115, 85)]

xmax = 600
xmitte = 300
ymax = 440

level = 12
w1 = 0.36   # Winkel 1
w2 = 0.48   # Winkel 2

def setup():
    size(640, 480)
    background(255)
    strokeWeight(1)
    noLoop()

def draw():
    drawPythagoras(-(xmax/10), 0, xmax/20, 0, level)

def drawPythagoras(a1, a2, b1, b2, level):
    if (level > 0):
        # Eckpunkte berechnen
        n1 = -b2 + a2
        n2 = -a1 + b1
        c1 = b1 + n1
        c2 = b2 + n2
        d1 = a1 + n1
        d2 = a2 + n2
        # Start-Rechteck zeichnen
        fill(palette[(level-1)%10])
        with beginClosedShape():
            vertex(a1 + xmitte, ymax - a2)
            vertex(b1 + xmitte, ymax - b2)
            vertex(c1 + xmitte, ymax - c2)
            vertex(d1 + xmitte, ymax - d2)
        e1 = d1 + w1*(c1 - d1) + w2*n1
        e2 = d2 + w1*(c2 - d2) + w2*n2
        # Schenkel-Quadrate zeichnen
        drawPythagoras(e1, e2, c1, c2, level-1)
        drawPythagoras(d1, d2, e1, e2, level-1)

Auch wenn es nicht nötig gewesen wäre, ich mag es einfach (und es dient der Übersichtlichkeit), wenn ich meine Processing.py-Sketche mit def setup() und def draw() gliedere. Mit noLoop() habe ich dann dafür gesorgt, daß die draw()-Schleife nur einmal abgearbeitet wird.

Erweiterungen und Änderungen

Einen »symmetrischen« Pythagoras-Baum erhält man übrigens, wenn man die beiden Winkel-Konstanten w1 und w2 jeweils auf 0.5 setzt.

Credits

Den rekursiven Algorithmus habe ich einem Pascal-Programm aus Jürgen Plate: Computergrafik: Einführung – Algorithmen – Programmentwicklung, München (Franzis) 2. Auflage 1988, Seiten 460-462 entnommen. Und die Geschichte des Baumes steht in dem schon mehrfach erwähnten Buch von Dieter Hermann, Algorithmen für Chaos und Fraktale, Bonn (Addison-Wesley) 1944 auf den Seiten 170f.