Exkurs: Zelluläre Automaten
Das Demokratie-Spiel
Spätestens seit der Wahl von Donald Trump zum Präsidenten der USA fragen sich ja einige, wie es dort mit der Demokratie bestellt sei. Dazu passend ein Spiel, das Peter Donelly vom University College of Swansea in Wales und Domenic Welsh von der Oxford University schon in den 80er Jahren des letzten Jahrhunderts untersucht hatten. Populär wurde es dann durch eine Veröffentlichung von Alexander K. Dewdney in der Scientific American und in der deutschen Schwesterzeitschrift Spektrum der Wissenschaft. Er nannte das Spiel »WAEHLER«:
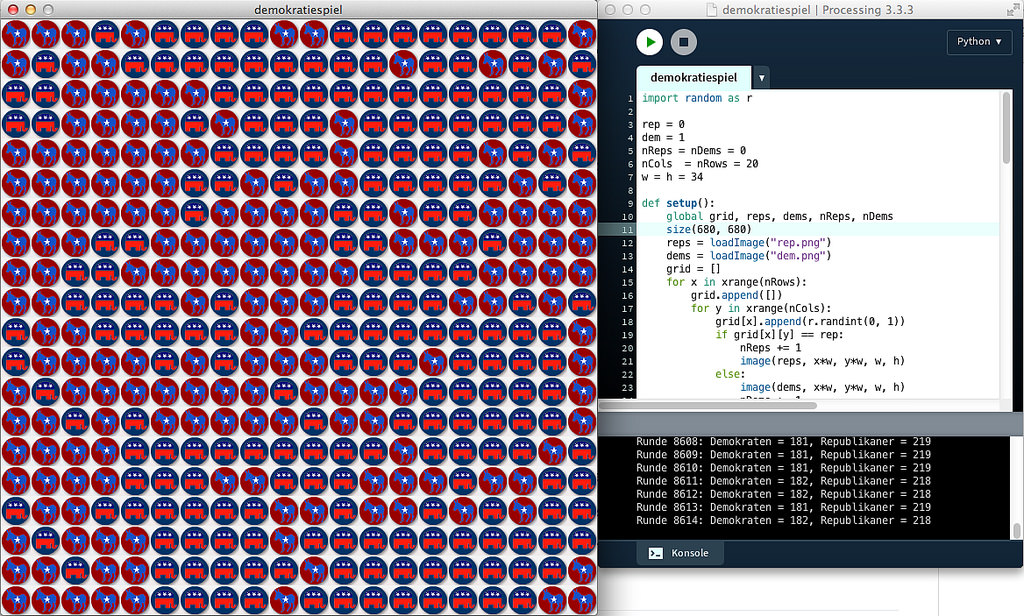
In diesem Spiel werden die Felder eines rechteckigen Feldes (hier 20 x 20 Felder) zuerst wahllos mit den Symbolen der Republikaner (Elephant) oder der Demokraten (Esel) besetzt. Das widerspiegelt die politische Einstellung der »Einwohner« dieses »Planeten«. Bei jedem Spielzug wird nun ein Einwohner in seiner politischen Meinung schwankend und nimmt die Einstellung eines seiner zufällig herausgegriffenen Nachbarn an (falls er nicht sowieso schon dessen Meinung ist).
Als Nachbarschaft gilt hier die Moore-Nachbarschaft, also alle 8 Nachbarfelder. Die Randbedingungen sind periodisch, das heißt jeder Spieler auf einem Randfeld hat »Nachbarn« auf der gegenüberliegenden Seite, die Spieler in den Eckfeldern sogar auf beiden gegenüberliegenden Seiten. Unser Spielfeld nimmt daher die Form eines Reifens oder eines Torus an, wie zum Beispiel auch in der populären Simulation WATOR.
Nun passiert Folgendes: Aus der anfänglich wüsten Verteilung bilden sich im Laufe des Spiels feste Inseln einer Meinung heraus. Und im Endeffekt gewinnt eine Partei die alleinige Herrschaft. Das geschieht manchmal sehr schnell, manchmal dauert es länger, weil sich einige Inseln des Widerstands hartnäckig halten, aber das Endergebnis ist immer gleich: Der Planet wird entweder komplett von Eseln oder komplett von Elephanten regiert. Ob das der Sinn einer Demokratie ist?
Das Spiel ist verwandt mit dem Selektions-Spiel, das Ruthild Winkler und Manfred Eigen schon 1975 in ihrem Buch »Das Spiel« vorgestellt hatten. Auch wenn die Regeln leicht abgewandelt sind, das Ergebnis ist stets das gleiche. Es überlebt immer nur eine Partei. Das ändert sich übrigens auch nicht, wenn man das Feld mit mehr als zwei Parteien beim Start füllt. Also ist nicht das amerikanische Wahlsystem die alleinige Ursache des Übels.
Der Code
Der Processing.py-Code ist straight forward. Lediglich die Behandlung der Randbedingungen ist allgemeiner gehalten, als unbedingt nötig. Damit sind bei Abwandlungen auch andere Nachbarschaften als die Moore-Umgebung möglich. Er folgt einem Processing- (Java-) Code, den ich vor Jahren schon einmal programmiert hatte.
import random as r
rep = 0
dem = 1
nReps = nDems = 0
nCols = nRows = 20
w = h = 34
def setup():
global grid, reps, dems, nReps, nDems
size(680, 680)
reps = loadImage("rep.png")
dems = loadImage("dem.png")
grid = []
for x in xrange(nRows):
grid.append([])
for y in xrange(nCols):
grid[x].append(r.randint(0, 1))
if grid[x][y] == rep:
nReps += 1
image(reps, x*w, y*w, w, h)
else:
image(dems, x*w, y*w, w, h)
nDems += 1
println("Start: Demokraten = " + str(nDems) + ",
Republikaner = " + str(nReps))
def draw():
global reps, dems, nReps, nDems
actorX = r.randint(0, nRows - 1)
actorY = r.randint(0, nCols - 1)
selection = r.randint(0, 7)
if selection == 0:
neighboorX = actorX
neighboorY = actorY - 1
elif selection == 1:
neighboorX = actorX + 1
neighboorY = actorY - 1
elif selection == 2:
neighboorX = actorX + 1
neighboorY = actorY
elif selection == 3:
neighboorX = actorX + 1
neighboorY = actorY + 1
elif selection == 4:
neighboorX = actorX
neighboorY = actorY + 1
elif selection == 5:
neighboorX = actorX - 1
neighboorY = actorY + 1
elif selection == 6:
neighboorX = actorX - 1
neighboorY = actorY
elif selection == 7:
neighboorX = actorX - 1
neighboorY = actorY - 1
else:
println("Irgend etwas ist gewaltig schiefgelaufen!")
# Prüfung der Ränder:
if neighboorX < 0:
neighboorX = nRows + neighboorX
neighboorX = neighboorX % nRows
if neighboorY < 0:
neighboorY = nCols + neighboorY
neighboorY = neighboorY % nCols
# Neuzeichnen des Spielfelds:
if grid[neighboorX][neighboorY] == dem:
if grid[actorX][actorY] != dem:
nDems += 1
nReps -= 1
grid[actorX][actorY] = dem
image(dems, actorX*w, actorY*w, w, h)
else:
if grid[actorX][actorY] != rep:
nReps += 1
nDems -= 1
grid[actorX][actorY] = rep
image(reps, actorX*w, actorY*w, w, h)
println("Runde " + str(frameCount) + ": Demokraten = "
+ str(nDems) + ", Republikaner = " + str(nReps))
if nDems == 0:
println("Die Republikaner haben nach " +
str(frameCount) + u" Runden die Macht übernommen!")
noLoop()
if nReps == 0:
println("Die Demokraten haben nach " +
str(frameCount) + u" Runden die Macht übernommen!")
noLoop()
Wer das Spiel selber nachprogrammieren möchte, hier gibt es auch noch die beiden Icons für die Republikaner (Elephant) und Demokraten (Esel):


Caveat
Ungeduldige sollten ert einmal mit einem 10x10-Gitter beginnen (size(340, 340)). Dann hat man in der Regel spätestens nach 20.000 Runden ein Ergebnis. Oder es kann sehr schnell gehen: Ich hatte auf diesem kleinen Gitter auch schon nach unter 2.000 Runden die absolute Herrschaft einer Partei erreicht. Auf einem 20x20-Gitter wie hier kann es durchaus 200.000 Runden und mehr dauern, bis die Diktatur kommt. Aber auf so einem großen Spielfeld erkennt man natürlich die stabilen »Inseln gleicher Meinung« sehr viel besser.
Es gibt sicher einen Schwellwert, der – wenn unterschritten – kein Zurück zur Macht mehr erlaubt. Aber er ist sehr klein: Ich habe es schon erlebt, daß sich Populationen, die unter die 10-Prozent-Marke gerutscht waren, sich wieder berappelten und im Endeffekt die Macht ergriffen.
Das ist das erste aus einer Reihe von (geplanten) Processing.py-Programmen, die sich mit Simulationen auf einem Gitter (aka »zelluläre Automaten«) beschäftigen.
Literatur
-
A.K. Dewdney: Wie man π erschießt. Fünf leichte Stücke für WHILE-Schleifen und Zufallsgenerator, oder: lebensechte Simulationen von Zombies, Wählern und Warteschlangen, in: Immo Diener (Hg.): Computer-Kurzweil, Heidelberg (Spektrum der Wissenschaft, Reihe: Verständliche Forschung) 1988
-
Manfred Eigen, Ruthild Winkler: Das Spiel. Naturgesetze steuern den Zufall, München (Piper), 1975 (unveränderte Taschenbuchausgabe 1985)
Frösche und Schildkröten oder: Wie entsteht Segregation?

Mitchel Resnick erzählt uns eine nette Geschichte: In einem Teich lebten Frösche und Schildkröten in trauter Eintracht zusammen. Jeder Frosch lebt auf einer Seerose und hat auf den acht benachbarten anliegenden Seerosen je vier Frösche und je vier Schildkröten als Nachbarn. (Man erkennt leicht, daß es sich um quadratische Seerosen mit einer Moore-Nachbarschaft handelt.) Doch eines Tages kommt ein böser Sturm auf und wirbelt alles durcheinander und auch etliche Frösche und Schildkröten kommen (zu gleichen Teilen) dabei um. Als sich der Sturm gelegt hat, versuchen die Tiere sich wieder zu organisieren und es sich auf den Seerosen gemütlich zu machen. Sie sind jedoch nur glücklich, wenn sie mindestens drei Nachbarn haben, die der gleichen Spezies angehören, ansonsten versuchen sie, eine andere, freie Seerose zu besiedeln. Und was passiert dabei? Es entstehen Kolonien, die nur von Schildkröten und andere Kolonien, die nur von Fröschen bevölkert werden. Eine vorbeifliegende Eule wundert sich und fragt einen Frosch, ob sie sich denn nicht mehr lieb haben würden. »Doch, wir haben uns lieb wie eh und je. Nur … es passiert einfach, daß wir zusammenziehen, unter der einzigen Voraussetzung, daß wir mindestens drei Nachbarn unserer Spezies haben wollen. Und den Schildkröten geht es genauso.«
Schauen wir uns das doch einfach einmal an:
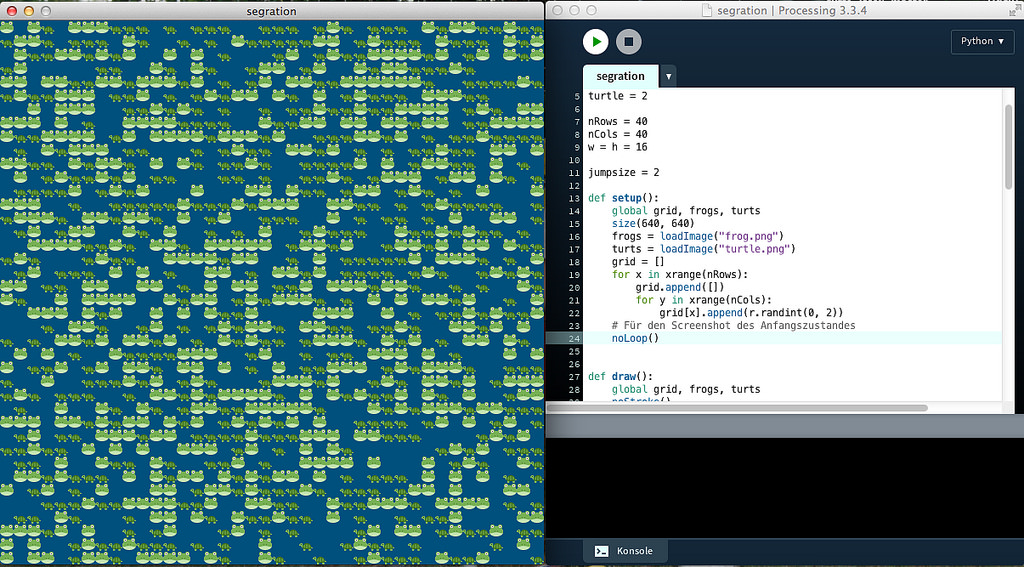
Resnick hat das natürlich in StarLogo programmiert, ich habe ein leicht abgewandeltes Processing.py-Programm geschrieben, mit dem man das Verhalten untersuchen kann. Beim Start verteilen wir zufällig die Schildkröten und Frösche zu gleichen Teilen auf einem 40x40-Raster, wobei etwa 30 Prozent leer bleiben, damit sich die Viecher auch bewegen können. In jedem Durchlauf wird zufällig ein Bewohner ausgewählt und er wird gefragt, ob er glücklich sei. Glücklich ist er nur, wenn er wenigstens drei Nachbarn hat, die der gleichen Spezies angehören. Ist er glücklich, bleibt er da sitzen wo er ist. Ist er unglücklich, sucht er zufällig in der Nachbarschaft in seiner Sprungdistanz (ja, in meiner Geschichte können auch Schildkröten springen) eine Seerose aus. Ist diese Seerose frei, springt er dahin, hoffend, dort glücklich zu werden. Ist das Feld nicht frei, bleibt er hocken und hofft auf eine neue Chance, wieder ausgewürfelt zu werden.
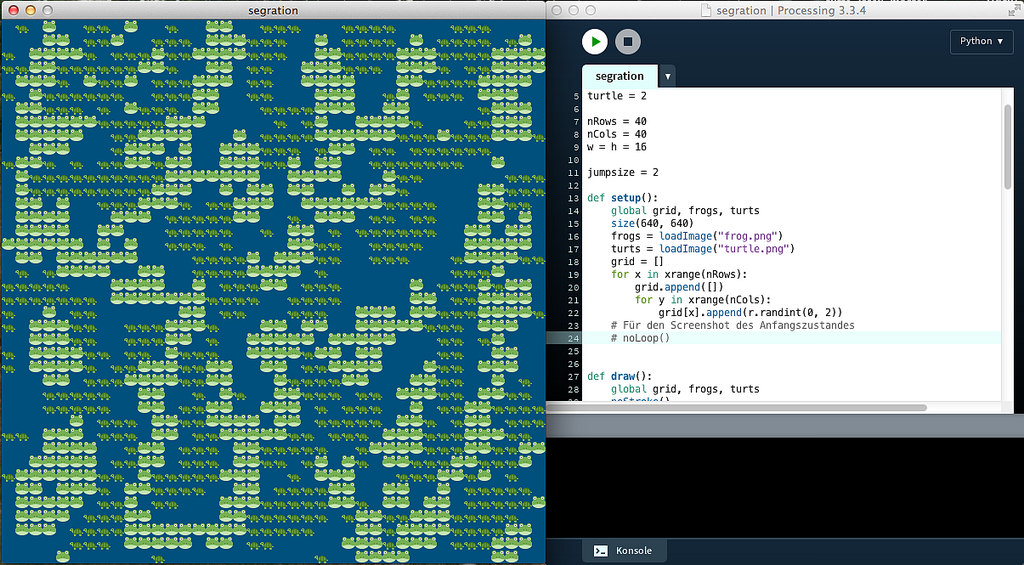
Läßt man diese Simulation nun laufen, stellt man fest, daß sich tatsächlich Cluster gleicher Spezies bilden. Die kleinste stabile Einheit ist ein Quadrat mit der Kantenlänge zwei – hier hat jeder mindestens drei Nachbarn. Außerdem ist eine Flucht von den Rändern weg zu beobachten. Hier habe ich einfach angenommen, daß das Wasser so flach ist, daß dort keine Seerosen gedeihen – die Ränder werden also nicht periodisch fortgesetzt. Und so hat man an den Rändern natürlich weniger Nachbarn und die Chance, glücklich zu sein, ist geringer.
Außerdem kann es vorkommen, daß einzelne Tiere regelrecht von der benachbarten Spezies eingekesselt werden und sie nicht mehr fliehen können. Die Armen sind zu einem ewigen Unglücklichsein verdammt. Hier hilft nur, die maximale Sprungdistanz zu erhöhen.
Überhaupt: Obige Screenshots stammen von einem Sketch mit einer Sprungdistanz von zwei, nachdem der Sektch etwa eine halbe Stunde gelaufen war. Es passiert nicht mehr viel. Die meisten zufällig ausgewählten in einer Runde sind glücklich und verharren auf ihren Platz. Nur noch wenige Exemplare einer Gattung irren umher und suchen Anschluß. Andere sind enteder vom Rand des Teiches oder von den Spezies der anderen Art eingekesselt und zu ewigem unglücklich sein verdammt.
Erhöht man aber den Wert der Sprungdistanz (zum Beispiel auf fünf), dann geht nicht nur die Clusterbildung schneller vonstatten, sondern auch die Zahl der eingekesselten Tiere geht massiv zurück.
Was uns dieses einfache Programm über die tatsächliche Segregation erzählt, überlasse ich aber der Phantasie meiner Leserinnen und Leser.
Der Quellcode
import random as r
empty = 0
frog = 1
turtle = 2
nRows = 40
nCols = 40
w = h = 16
jumpsize = 2
def setup():
global grid, frogs, turts
size(640, 640)
frogs = loadImage("frog.png")
turts = loadImage("turtle.png")
grid = []
for x in xrange(nRows):
grid.append([])
for y in xrange(nCols):
grid[x].append(r.randint(0, 2))
# Für den Screenshot des Anfangszustandes
# noLoop()
def draw():
global grid, frogs, turts
noStroke()
background(0, 80, 125)
for x in xrange(nRows):
for y in xrange(nCols):
if grid[x][y] == empty:
fill(0, 80, 125)
rect(x*w, y*h, w, h)
elif grid[x][y] == frog:
image(frogs, x*w, y*h, w, h)
elif grid[x][y] == turtle:
image(turts, x*w, y*h, w, h)
else:
println("Etwas ist falsch im Staate Lilypond!")
actorX = r.randint(0, nRows-1)
actorY = r.randint(0, nCols-1)
# Lebt hier jemand?
if grid[actorX][actorY] > 0:
# Und ist er glücklich?
happy = isHappy(grid[actorX][actorY], actorX, actorY)
# Wenn nicht, dann möglichst weg von hier
if not(happy):
newX = r.randint(-jumpsize, jumpsize)
newY = r.randint(-jumpsize, jumpsize)
newX += actorX
newY += actorY
# Liegt mein Ziel noch im Teich?
if ((newX >= 0) and (newX < nRows)
and (newY >= 0) and (newY < nCols)):
if grid[newX][newY] == empty:
grid[newX][newY] = grid[actorX][actorY]
grid[actorX][actorY] = empty
def isHappy(animal, x, y):
happy = 0
if (y-1 > 0) and (grid[x][y-1] == animal):
happy += 1
if (x+1 < nRows) and (y-1 > 0) and (grid[x+1][y-1] == animal):
happy += 1
if (x+1 < nRows) and (grid[x+1][y] == animal):
happy += 1
if (x+1 < nRows) and (y+1 < nCols) and (grid[x+1][y+1] == animal):
happy += 1
if (y+1 < nCols) and (grid[x][y+1] == animal):
happy += 1
if (x-1 > 0) and (y+1 < nCols) and (grid[x-1][y+1] == animal):
happy += 1
if (y+1 < nCols) and (grid[x][y+1] == animal):
happy += 1
if (x-1 > 0) and (grid[x-1][y] == animal):
happy += 1
if happy >= 3:
return True
else:
return False
Die Bilder von Frosch und Schildkröte habe ich den Twitter-Emojis entnommen und hier sind sie noch einmal, damit Ihr das Spiel nachprogrammieren könnt:


Literatur
- Mitchel Resnick: Turtles, Termites, and Traffic Jams: Explorations in Massively Parallel Microworlds, Cambridge, MA (MIT Press) 1997, p. 81 - 88
Der Waldbrand-Simulator
Bei dem Demokratie-Spiel und bei den Experimenten mit den Fröschen und Schildkröten änderte sich pro Durchlauf jeweils nur das Verhalten einer Zelle in Abänggkeit von ihren direkten Nachbarn und war für den weiteren Verlauf der Simulation verantwortlich. Bei den meisten Simulationen mit zellulären Automaten jedoch wird der neue Wert aller Zellen in Abhängigkeit von den Nachbarn betrachtet und neu berechnet. Dafür muß man dann zwei Arrays anlegen, eines, das die aktuellen und eines das die zukünftigen Werte beinhaltet. Ich möchte das mal am Beispiel einer beliebten Simulation zeigen, der Simulation eines Waldbrandes mit einem zellulären Automaten.
Die Regeln dieser Simulation folgen der Beschreibung, die Daniel Scholz in seinem Buch »Pixelspiele«1 gegeben hat:
Kein Spiel ohne Regeln
Für alle Zellen xij gelten folgende Regeln:
- Befindet sich xij im Zustand leer (empty), dann wächst auf xij mit einer Wahrscheinlichkeit
aein Baum, so daß der Zustand von xij im nächsten Schritt tree ist. - Befindet sich xij im Zustand Baum (tree), und mindestens eine Zelle in der Nachbarschaft ist im Zustand Feuer (burning), dann brennt auch xij, so daß der Zustand von xij im nächsten Schritt auch burning ist.
- Automatischer Ablauf: Falls xij ein Baum ist und keiner seiner Nachbarn brennt, dann wird xij mit einer Wahrscheinlichkeit von
gvon einem Blitz getroffen, so daß xij im nächsten Schritt ebenfalls burning ist. - Interaktive Version: Wird die Zelle xij mit dem Mauszeiger angeklickt, dann wird xij von einem Blitz getroffen und der Zustand von xij ist im nächsten Schritt burning.
- Befindet sich die Zelle xij im Zustand burning, dann erlischt das Feuer und der Zustand von xij ist im nächsten Schritt empty.
- Trifft keine der obigen Regeln zu, dann verändert sich der Zustand der Zelle xij im nächsten Schritt nicht.
Als Nachbarschaft wird die Von-Neumann-Nachbarschaft angenommen, Nachbarn sind also nur die direkten Zellen oben und unten sowie rechts und links, das heißt, jede Zelle hat genau vier Nachbarn.
Als Randbedingung wurde ein geschlossener Rand gewählt, daß heißt die Zellen am Rande des Feldes werden in der Simulation gar nicht berücksichtigt, sie bleiben auf ewig, wie sie sind. Daher habe ich bei der Initialisierung des Feldes mit
if ((x > 0) and (y > 0) and (x < nRows-1)
and (y < nCols-1) and randint(0, 10000) <= 2000):
grid[x].append(tree)
else:
grid[x].append(empty)
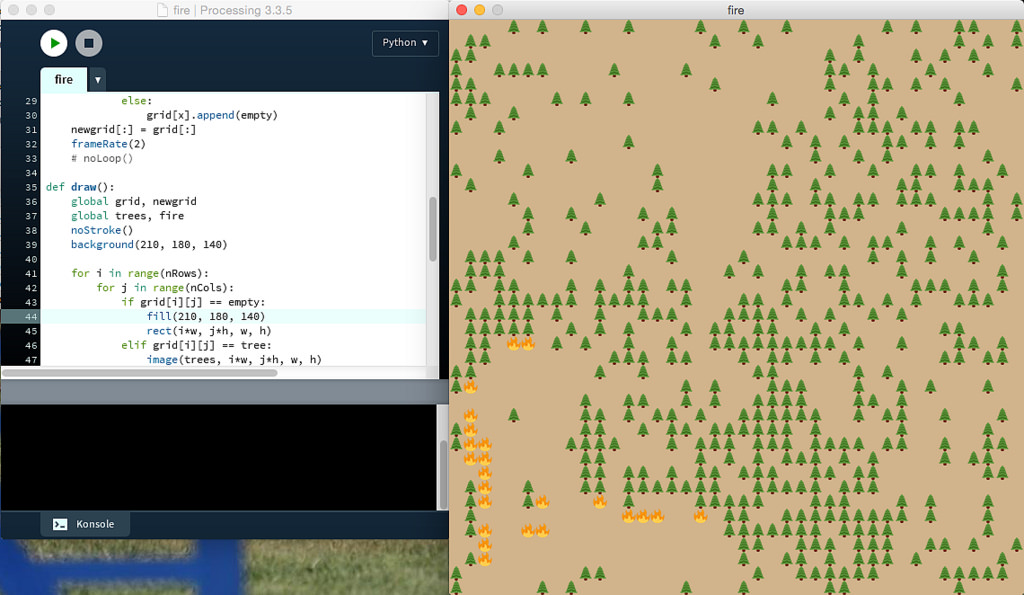
dafür gesorgt, daß die Randfelder immer leer sind. Das hat auf den Simulationsverlauf keinen Einfluß, aber es störte mich besonders bei der Darstellung mit den Emojis, daß auf den Rändern anfangs immer ein paar Bäume dumm herum standen, wie noch im obigen Screenshot dokumentiert, der während einer frühen Phase der Realisierung dieser Simulation enstand.
Die Realisierung
Oben habe ich es schon angesprochen, für die erste Version der Waldbrandsimulation habe ich wieder Twitters Twemojis geplündert und hier sind die Bildchen vom Baum und vom Feuer, damit Ihr die Simulation nachprogrammieren könnt:


Wenn Ihr die Bilder herunterladet, beachtet bitte, daß ich, weil es schon ein anderes Baumbildchen gab, dieses hier tree2.png nennen mußte. Im Sketch heißt es aber tree.png, Ihr müßt also entweder die Bezeichnung im Sketch ändern (nicht gut) oder einfach den Namen des Bildchens ändern (besser). Es sind winzige, 16x16 Pixel große Bildchen und das Spielfeld habe ich diesen Ausmaßen angepaßt:
def setup():
global trees, fire
size(640, 640)
background(210, 180, 140)
trees = loadImage("tree.png")
fire = loadImage("fire.png")
for x in range(nRows):
grid.append([])
newgrid.append([])
for y in range(nCols):
# Randbedingungen
if ((x > 0) and (y > 0) and (x < nRows-1)
and (y < nCols-1) and randint(0, 10000) <= 2000):
grid[x].append(tree)
else:
grid[x].append(empty)
newgrid[:] = grid[:]
frameRate(2)
Eine frameRate() von 2 ist durchaus ausreichend, sonst läuft die Simulation so schnell, daß Ihr gar nichts nachvollziehen könnt.
Aber ganz zu Beginn habe ich randint für die Zufallszahlen importiert, ein paar Konstanten gesetzt und die beiden Arrays initialisiert:
from random import randint
empty = 0
tree = 1
burning = 20
a = 40
g = 1
nRows = 40
nCols = 40
w = h = 16
grid = []
newgrid = []
Die draw()-Funktion ist in allen Simulationen gleich,
draw():
global grid, newgrid
global trees, fire
noStroke()
background(210, 180, 140)
for i in range(nRows):
for j in range(nCols):
if grid[i][j] == empty:
fill(210, 180, 140)
rect(i*w, j*h, w, h)
elif grid[i][j] == tree:
image(trees, i*w, j*h, w, h)
elif grid[i][j] == burning:
image(fire, i*w, j*h, w, h)
calcNext()
der Unterschied für den per Zufall generierten Blitzeinschlag, respektive den durch Nutzereingabe verursachten Blitz, liegt in der Funktion calcNext(). Hier erst einmal die nicht interaktive Version:
calcNext():
global grid, newgrid
newgrid[:] = grid[:]
# Next Generation
for i in range(1, nRows-1):
for j in range(1, nCols-1):
if grid[i][j] == burning:
newgrid[i][j] = empty
# Brennt ein Nachbar?
if grid[i-1][j] == tree:
newgrid[i-1][j] = burning
if grid[i][j-1] == tree:
newgrid[i][j-1] = burning
if grid[i][j+1] == tree:
newgrid[i][j+1] = burning
if grid[i+1][j] == tree:
newgrid[i+1][j] = burning
elif grid[i][j] == empty:
if randint(0, 10000) < a:
newgrid[i][j] = tree
if grid[i][j] == tree:
# Schlägt ein Blitz ein?
if (random(10000) < g):
newgrid[i][j] = burning
grid[:] = newgrid[:]
Mit for i in range(1, nRows-1) und for j in range(1, nCols-1) habe ich die Randfelder von der Abfrage ausgeschlossen und somit die Randbedingung »geschlossener Rand« erfüllt.
In den vorletzten zwei Zeilen wird die Wahrscheinlichkeit abgefragt, ob ein Blitz einschlägt und wenn diese (geringe) Wahrscheinlichkeit zutrifft, dann wird das Feld xij für den nächsten Zustand auf brennend (burning) gesetzt. In der interaktiven Variante entfallen diese beiden Zeilen, dafür kommt noch die Funktion mousePressed() hinzu,
def mousePressed():
newgrid[mouseX/16][mouseY/16] = burning
die einfach für die Zelle, in der die Maus klickt, den neuen Zustand auf burning setzt.
Der Quellcode (1)
Bevor ich weitermache, erst einmal den Quellcode des vollständigen Programmes in der interaktiven Version:
from random import randint
empty = 0
tree = 1
burning = 20
a = 40
g = 1
nRows = 40
nCols = 40
w = h = 16
grid = []
newgrid = []
def setup():
global trees, fire
size(640, 640)
background(210, 180, 140)
trees = loadImage("tree.png")
fire = loadImage("fire.png")
for x in range(nRows):
grid.append([])
newgrid.append([])
for y in range(nCols):
# Randbedingungen
if ((x > 0) and (y > 0) and (x < nRows-1)
and (y < nCols-1) and randint(0, 10000) <= 2000):
grid[x].append(tree)
else:
grid[x].append(empty)
newgrid[:] = grid[:]
frameRate(2)
# noLoop()
def draw():
global grid, newgrid
global trees, fire
noStroke()
background(210, 180, 140)
for i in range(nRows):
for j in range(nCols):
if grid[i][j] == empty:
fill(210, 180, 140)
rect(i*w, j*h, w, h)
elif grid[i][j] == tree:
image(trees, i*w, j*h, w, h)
elif grid[i][j] == burning:
image(fire, i*w, j*h, w, h)
calcNext()
def calcNext():
global grid, newgrid
newgrid[:] = grid[:]
# Next Generation
for i in range(1, nRows-1):
for j in range(1, nCols-1):
if grid[i][j] == burning:
newgrid[i][j] = empty
# Brennt ein Nachbar?
if grid[i-1][j] == tree:
newgrid[i-1][j] = burning
if grid[i][j-1] == tree:
newgrid[i][j-1] = burning
if grid[i][j+1] == tree:
newgrid[i][j+1] = burning
if grid[i+1][j] == tree:
newgrid[i+1][j] = burning
elif grid[i][j] == empty:
if randint(0, 10000) < a:
newgrid[i][j] = tree
grid[:] = newgrid[:]
def mousePressed():
newgrid[mouseX/16][mouseY/16] = burning
Für die automatisch ablaufende Fassung müßt Ihr einfach nur die oben erwähnten zwei Zeilen vor
grid[:] = newgrid[:]
in die Funktion calcNext() einfügen und die Funktion mousePressed() löschen.
Ein größerer Wald
Die obige Simulation läuft schon sehr zufriedenstellend ab, aber um Muster zu erkennen, muß man den »Wald« doch weiter vergrößern. Ich habe in einer neuen Version dieser Simulation das Spielfeld daher auf 280x160 Zellen erweitert. Damit mein Monitor nicht gesprengt wird, sind diese Zellen jetzt nur noch 2x2 Pixel groß, was zu einer Fenstergröße von 560x320 führt.
Die Zellen werden jetzt nicht mehr durch Emojis dargestellt, sondern durch kleine Rechtecke in verschiedenen Farben. Da ich leicht farbenblind bin, habe ich mir die Farben aus einer Tabelle mit Farbnamen zusammengsucht, ein leeres Feld sollte daher ockerfarben dargestellt werden, ein Feld mit einem Baum dunkelgrün und ein brennendes Feld in einem leuchtenden rot. Diese Angaben sind ohne Gewähr, aber Ihr könnt die Farben ja im Zweifelsfalle selber Euren Wünschen anpassen.
Beispielsimulation






Wenn Ihr diese Simulation über einen gewissen Zeitraum laufen laßt, dann erkennt Ihr, daß sich im Laufe der Zeit ein gewisses, wenn auch schwankendes Gleichgewicht zwischen Wald und freier Fläche einstellt. Dieses Gleichgewicht soll sich sogar relativ unabhängig von den gewählten Parametern einstellen (das ist allerdings in der Literatur umstritten). In den obigen Schreenshots, die ich mit
if (frameCount % 50) == 0:
print(frameCount)
saveFrame("frames/fire-gen-####.png")
erstellt habe, könnt Ihr sehen, wie sich die Simulation nach je 50 Schritten verändert hat und nach einer ruhigen Anfangsphase des Wachstums scheint der Gleichgewichtszustand tatsächlich erreicht. Generation 150 und Generation 300 sind sich sehr ähnlich, dazwischen brennt der Wald erst heftiger (Generation 200) und erlebt dann wieder eine Phase des Wachstums (Generation 250).
Der Quellcode (2)
Probiert es – auch mit anderen Paramtern für a und g einfach mal aus. Darum hier der komplette Quellcode dieser Version:
from random import randint
empty = 0
tree = 1
burning = 20
a = 40
g = 1
nRows = 280
nCols = 160
w = h = 2
grid = []
newgrid = []
def setup():
global trees, fire
size(560, 320)
background(210, 180, 140)
for x in range(nRows):
grid.append([])
newgrid.append([])
for y in range(nCols):
# Randbedingungen
if ((x > 0) and (y > 0) and (x < nRows-1)
and (y < nCols-1) and randint(0, 10000) <= 2000):
grid[x].append(tree)
else:
grid[x].append(empty)
newgrid[:] = grid[:]
frameRate(10)
# noLoop()
def draw():
global grid, newgrid
global trees, fire
noStroke()
background(210, 180, 140)
for i in range(nRows):
for j in range(nCols):
if grid[i][j] == empty:
fill(210, 180, 140)
rect(i*w, j*h, w, h)
elif grid[i][j] == tree:
fill(0, 100, 0)
rect(i*w, j*h, w, h)
elif grid[i][j] == burning:
fill(255, 69, 0)
rect(i*w, j*h, w, h)
if (frameCount % 50) == 0:
print(frameCount)
saveFrame("frames/fire-gen-####.png")
calcNext()
def calcNext():
global grid, newgrid
newgrid[:] = grid[:]
# Next Generation
for i in range(1, nRows-1):
for j in range(1, nCols-1):
if grid[i][j] == burning:
newgrid[i][j] = empty
# Brennt ein Nachbar?
if grid[i-1][j] == tree:
newgrid[i-1][j] = burning
if grid[i][j-1] == tree:
newgrid[i][j-1] = burning
if grid[i][j+1] == tree:
newgrid[i][j+1] = burning
if grid[i+1][j] == tree:
newgrid[i+1][j] = burning
elif grid[i][j] == empty:
if randint(0, 10000) < a:
newgrid[i][j] = tree
if grid[i][j] == tree:
# Schlägt ein Blitz ein?
if (random(10000) < 1):
newgrid[i][j] = burning
grid[:] = newgrid[:]
Er unterscheidet sich nicht grundlegend von den vorherigen Versionen, daher sollten Sie ihn durchaus nachvollziehen können.
Caveat
Ich glaube nicht wirklich, daß diese Simualtion ein realistisches Bild von Waldbränden liefert, dazu fehlen zum Beispiel Parameter für die Windrichtung, manche Bäume brennen leichter als andere und vieles mehr. Aber es ist eine nette Spielerei und Ihr seid durchaus aufgefordert, die fehlenden Parameter einzufügen und damit zu spielen. Der Aufsatz »Simulating the World in Emojis« den Nicky Case im Januar 2016 veröffentlichte, gibt dafür – aber auch für weitere Simualtionen – nette Anregungen.
-
Daniel Scholz: Pixelspiele, Modellieren und Simulieren mit zellulären Automaten, Berlin - Heidelberg (Springer Spektrum) 2014, S. 19-25 ↩