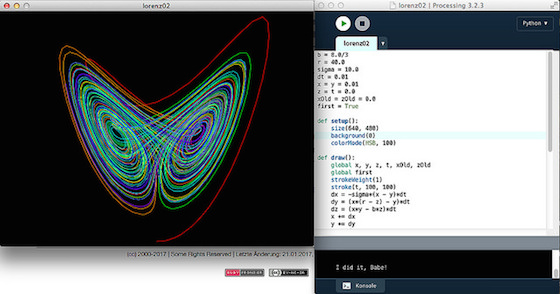
Der Lorenz-Attraktor, eine Ikone der Chaos-Theorie

Nachdem ich im letzten Abschnitt die Schmetterlingskurve mit Processing.py gezeichnet hatte, wollte ich nun darauf aufbauen und eine Ikone der Chaos-Forschung, den Lorenz-Attraktor damit zeichnen. Ich hatte das ja auch schon einmal mit R getan – dort findet Ihr auch weitere Hintergrundinformationen zu diesem Attraktor –, aber mit R wurde nur das fertige Ergebnis visualisiert. Hier kommt es mir aber wieder darauf an, die Entstehung der Kurve verfolgen zu können und dafür ist, wie schon bei der Schmetterlingskurve, Processing gut geeignet:

Screenshot

Als einer der ersten hatte 1961 Edward N. Lorenz, ein Meteorologe am Massachusetts Institute of Technology (MIT), erkannt, daß Iteration Chaos erzeugt. Er benutzte dort einen Computer, um ein einfaches nichtlineares Gleichungssystem zu lösen, das ein simples Modell der Luftströmungen in der Erdatmosphäre simulieren sollte. Dazu benutzte er ein System von sieben Differentialgleichungen, das Barry Saltzman im gleichen Jahr aus den Navier-Stokes-Gleichungen 1 hergeleitet hatte. Für dieses System existierte keine analytische Lösung, also mußte es numerisch (d.h. wie damals und auch heute noch vielfach üblich in FORTRAN) gelöst werden. Lorenz hatte entdeckt, daß bei nichtperiodischen Lösungen der Gleichungen vier der sieben Variablen gegen Null strebten. Daher konnte er das System auf drei Gleichungen reduzieren:

$$ \begin{align} \frac{dx}{dt} & = -\sigma (y - z) \\ \frac{dy}{dt} & = (\rho - z)x - y \\ \frac{dz}{dt} & = xy - \gamma z \end{align} $$

Dabei sind \(\sigma = -10\), \(\rho = 40\) und \(\gamma = - \frac{8}{3}\). Die Parameter der Gleichung habe ich [Herm1994] entnommen, [Stew1993] gibt \(\rho = 28\) an, aber der Wert ändert nichts an dem Verhalten der Kurve und \(\rho = 40\) füllt das Fenster einfach besser aus. 😜

Processing.py besitzt im Gegensatz zu R oder NumPy kein Modul zur numerischen Lösung von Differentialgleichungen und so habe ich das einfache Eulersche Poligonzugverfahren zur numerischen Berechnung benutzt

    dx = -sigma*(x - y)*dt
    dy = (x*(r - z) - y)*dt
    dz = (x*y - b*z)*dt
    x += dx
    y += dy
    z += dz

und dabei konstant dt = 0.01 gesetzt. Das benötigt natürlich mehr Rechenkapazität, als sie Lorenz je zur Verfügung standen, aber trotz der größeren Genauigkeit ändert sich nichts am chaotischen Verhalten der Kurve. Für die Farbberechnugn habe ich dieses mal nur den Farbwert (Hue) bei jeder Iteration geändert, Sättigung (Saturation) und Helligkeit (Brightness) bleiben konstant auf dem höchsten Wert. Das ergibt kräftige Farben, die von Rot über Orange nach Gelb und dann nach Grün, Blau und Violett wandern. So kann man schön erkennen, daß die beiden »Flügel« des Attraktors immer wieder, aber für uns unvorhersehbar, durchlaufen werden.

Der Quellcode

Hier nun der vollständige Quellcode des Skripts. Er ist kurz und selbsterklärend und folgt weitestgehend dem Pascal-Programm aus [Herm1994], Seiten 80ff.

b = 8.0/3
r = 40.0
sigma = 10.0
dt = 0.01
x = y = 0.01
z = t = 0.0
xOld = zOld = 0.0
first = True

def setup():
    size(640, 480)
    background(0)
    colorMode(HSB, 100)

def draw():
    global x, y, z, t, xOld, zOld
    global first
    strokeWeight(1)
    stroke(t, 100, 100)
    dx = -sigma*(x - y)*dt
    dy = (x*(r - z) - y)*dt
    dz = (x*y - b*z)*dt
    x += dx
    y += dy
    z += dz
    # auf Fenstergröße skalieren
    xx = (x*8) + 320
    zz = 470 - (z*5.5)
    if first:
        point(xx, zz)
    else:
       line(xOld, zOld, xx, zz)
    xOld = xx
    zOld = zz
    first = False 
    t = t + dt
    if ( t >= 75.0):
       print("I did it, Babe!")
       noLoop()
 

Literatur

  1. Eine sehr schöne Einführung in das ungelöste Problem der Navier-Stokes-Gleichungen gibt es von Florian Freistetter in der 217. Folge seiner Sternengeschichten ↩