Wir backen uns ein Mandelbrötchen

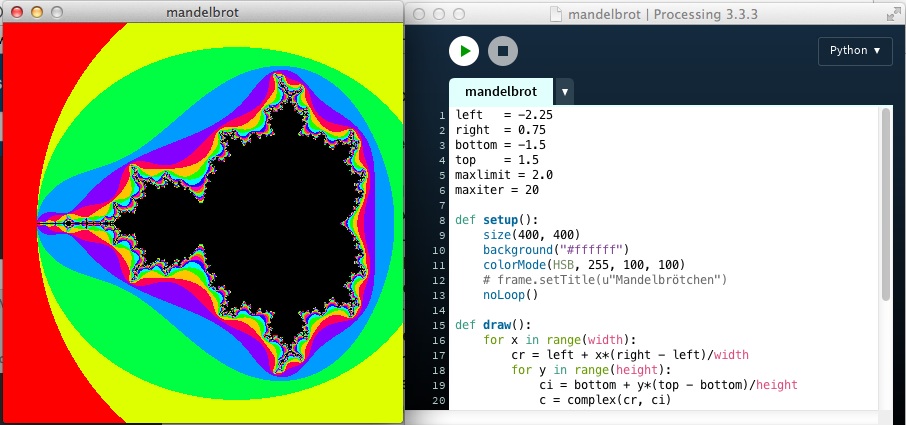
Die Mandelbrot-Menge ist die zentrale Ikone der Chaos-Theorie und das Urbild aller Fraktale. Sie ist die Menge aller komplexen Zahlen c, für welche die durch

$$ \begin{align} z_{0} & = 0\\ z_{n+1} & = z_{n}^{2}+c\\ \end{align} $$

rekursiv definierte Folge beschränkt ist. Bilder der Mandelbrot-Menge können erzeugt werden, indem für jeden Wert des Parameters c, der gemäß obiger Rekursion endlich bleibt, ein Farbwert in der komplexen Ebene zugeordnet wird.

Die komplexe Ebene wird in der Regel so dargestellt, daß in der Horizontalen (in der kartesisschen Ebene die x-Achse) der Realteil der komplexen Zahl und in der Vertikalen (in der kartesischen Ebene die y-Achse) der imaginäre Teil aufgetragen wird. Jede komplexe Zahl entspricht also einen Punkt in der komplexen Ebene. Die zur Mandelbrotmenge gehörenden Zahlen werden im Allgemeinen schwarz dargestellt, die übrigen Farbwerte werden der Anzahl von Iterationen (maxiter) zugeordnet, nach der der gewählte Punkt der Ebene einen Grenzwert (maxlimit) verläßt. Der theoretische Grenzwert ist 2.0, doch können besonders bei Ausschnitten aus der Menge, um andere Farbkombinationen zu erreichen, auch höhere Grenzwerte verwendet werden. Bei Ausschnitten muß auch die Anzahl der Iterationen massiv erhöht werden, um eine hinreichende Genauigkeit der Darstellung zu erreichen.

Das Programm

Python kennt den Datentyp complex und kann mit komplexen Zahlen rechnen. Daher drängt sich die Sprache für Experimente mit komplexen Zahlen geradezu auf. Zuert werden mit cr und ci Real- und Imaginärteil definiert und dann mit

c = complex(cr, ci)

die komplexe Zahl erzeugt. Für die eigentliche Iteration wird dann – nachdem der Startwert z = 0.0 festgelegt wurde – nur eine Zeile benötigt:

z = (z**2) + c

Wie schon in anderen Beispielen habe ich für die Farbdarstellung den HSB-Raum verwendet und über den Hue-Wert iteriert. Das macht alles schön bunt, aber es gibt natürlich viele Möglichkeiten, ansprechendere Farben zu bekommen, beliebt sind zum Beispiel selbsterstellte Paletten mit 256 ausgesuchten Farbwerten, die entweder harmonisch ineinander übergehen oder bestimmte Kontraste betonen.

Der komplette Quellcode

left   = -2.25
right  = 0.75
bottom = -1.5
top    = 1.5
maxlimit = 2.0
maxiter = 20

def setup():
    size(400, 400)
    background("#ffffff")
    colorMode(HSB, 255, 100, 100)
    # frame.setTitle(u"Mandelbrötchen")
    noLoop()

def draw():
    for x in range(width):
        cr = left + x*(right - left)/width
        for y in range(height):
            ci = bottom + y*(top - bottom)/height
            c = complex(cr, ci)
            z = 0.0
            i = 0
            for i in range(maxiter):
                if abs(z) > maxlimit:
                    break
                z = (z**2) + c
                if i == (maxiter - 1):
                    set(x, y, color(0, 0, 0))
                else:
                    set(x, y, color((i*48)%255, 100, 100))

Um zu sehen, wie sich die Farben ändern, kann man durchaus mal mit den Werten von maxlimit spielen und diesen zum Beispiel auf 3.0 oder 4.0 setzen. Auch die Erhöhung der Anzahl der Iterationen maxiter verändert die Farbzuordnung, verlängert aber auch die Rechhenzeit drastisch, so daß man speziell bei Ausschnitten aus der Mandelbrotmenge schon einige Zeit auf das Ergebnis warten muß.