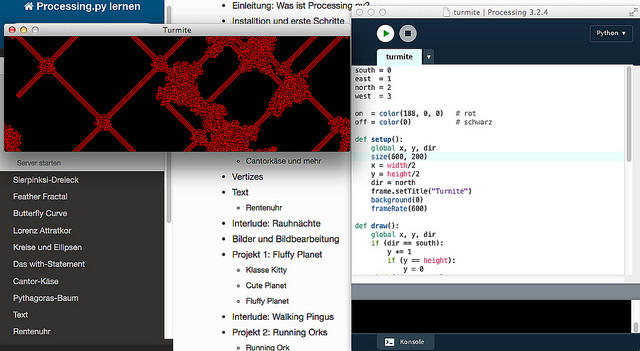
Turmite

Turmiten sind quadratische, 1x1 Pixel große, kybernetische Kreaturen mit einer höchst kümmerlichen Andeutung eines Gehirns. Sie können die Farben des Pixels oder der Zelle, auf der sie gerade stehen, erkennen und danach handeln. Ist die Zelle schwarz, färben sie sie rot und bewegen sich um ein Feld nach links. Ist die Farbe rot, färben sie die Zelle schwarz und bewegen sich um ein Feld nach rechts.

Wird solch eine Turmite auf eine schwarze, unendlichen Ebene gesetzt, erzeugt sie zuerst ein chaotisches Muster. Doch nach ungefähr 10.000 Schritten bildet sie auf einmal eine Turmiten-Autobahn, eine regelmäßige Struktur, die immer nach 104 Schritten in denselben Zustand zurückkehrt, nur jeweils um 2 Felder verschoben.

Die Turmite programmieren

Ich habe eine dieser Turmiten in einem Processing.py-Sketch zum Leben erweckt. Damit sie nicht in der Unendlichkeit der Ebene entfleucht, habe ich die Ecken des Fensters miteinander verklebt und sie so in eine Torus-Welt verwandelt. Wenn die Turmite am unteren Ende des Fensters verschwindet, taucht sie am oberen Ende wieder auf, verschwindet sie am rechten Rand erscheint sie wieder am linken Rand. Für beide Ränder gilt das natürlich auch umgekehrt, die Welt der Turmite ist also ein fett aufgeblasener Fahrradschlauch, auf dem sie sich entlang bewegt.

Den Farbsensor der Turmite habe ich mit dem Processing-Befehl get(x, y) simuliert. Er liest die Farbe des Pixels. Analog dazu gibt es die Funktion set(x, y, color), die die Farbe color an die Stelle x, y schreibt. Die beiden Farben habe ich im Sketch on für schwarz und off für rot genannt. Ich bin von der Metapher ausgegangen, daß die Turmite auf der schwarzen Ebene ein Feld entweder einschaltet (also rot färbt) oder es wieder ausschaltet (es wird wieder schwarz).

Als ich damals auf meinem Atari-ST mein erstes Turmitenprogramm schrieb, dauerte es ewig, bis die Turmite mit ihrer Autobahn im Unendlichen verschwunden war (sie das Bildschirmfenster verlassen hatte). An eine Rückkehr via Torus wagte ich nicht zu denken, dafür reichte meine Geduld nicht aus. Nun in Processing.py habe ich die Framerate auf 600 gesetzt und so geht es doch recht schnell voran.

Interessant ist, daß die Turmite, wenn sie auf eine von ihr geschaffene Autobahn trifft, zwar erst einmal wieder ein chaotisches Verhalten an den Tag legt, aber über kurz oder lang wieder eine Autobahn baut. Diese Turmiten-Autobahnen kennen nur zwei Orientierungen, sie verlaufen entweder parallel oder stehen senkrecht aufeinander.

Quellcode

Nach dem oben Beschriebenen dürfte der Quellcode leicht verständlich sein. In der setup()-Funktion wird die Hintergrundfarbe auf schwarz und die Turmite in die Mitte des Fensters mit der Ausrichtung nach Norden gesetzt.

Im ersten Abschnitt der draw()-Funktion wird die Turmite gemäß Ihrer aktuellen Orientierung bewegt und die Behandlung der Fensterränder berücksichtigt. Dann wird die Farbe der aktuellen Zelle gelesen (mit get(x, y)) und je nach Zustand eine neue Farbe gesetzt und die Orientierung der Turmite den Regeln entsprechend geändert. Das ist alles.

south = 0
east  = 1
north = 2
west  = 3

on  = color(188, 0, 0)   # rot
off = color(0)           # schwarz

def setup():
    global x, y, dir
    size(600, 200)
    x = width/2
    y = height/2
    dir = north
    frame.setTitle("Turmite")
    background(0)
    frameRate(600)

def draw():
    global x, y, dir
    if (dir == south):
        y += 1
        if (y == height):
            y = 0
    elif (dir == east):
        x += 1
        if (x == width):
            x = 0
    elif (dir == north):
        if (y == 0):
            y = height - 1
        else:
            y -= 1
    elif (dir == west):
        if (x == 0):
            x = width - 1
        else:
            x -= 1

    if (get(x, y) == on):
        set(x, y, off)
        if (dir == south):
            dir = west
        else:
            dir -= 1
    else:
        set(x, y, on)
        if (dir == west):
            dir = south
        else:
            dir += 1

Weitere mögliche Experimente

Die Turmiten gehen auf Greg Turk zurück, der damals Doktorand an der Universität von North Carolina in Chapel Hill war. Er zeigte, daß sie eine zweidimensionale Turingmaschine sind. Später hat sie Christopher Langton weiterentwickelt und beschrieben – daher ist sie auch unter dem Namen »Langtons Ameise« (Lanton's Ant) bekannt. Die hier vorgestellte ist die einfachste Form solch einer Ameise. Ein nächster Schritt wäre beispielsweise, die Welt mit zwei Turmiten zu bevölkern, die eine färbt die Ebene rot, wenn sie auf ein schwarzes Feld trifft, die andere färbt sie blau. Natürlich müßten dann beide Ameisen auch Regeln implementiert bekommen, wie sie zu verfahren haben, wenn sie auf ein blaues respektive ein rotes Feld treffen.

Von Turk selber gibt es zum Beispiel eine Turmite mit zwei Zuständen, nennen wir diese A und B und mit folgendem Regelsatz:

Zustand	A	B
grün	schwarz, vorwärs, B	grün, rechts, A
schwarz	grün, links, A	grün, rechts, A

Sie erzeugt ein Spiralmuster, »immer größer werdende strukturierte Gebiete, die sich in regelmäßiger Anordnung um einen Startpunkt winden«.

Eine weitere Turmite, die mit vier Farben hantiert, braucht nur einen Zustand, um ebenfalls ein interessantes, symmetrisches Muster zu bilden. Hier ihr Regelsatz:

Zustand	A
blau	rot, rechts, A
rot	gelb, rechts, A
gelb	grün, links, A
grün	blau, links, A

Es gibt also noch viel zu entdecken in der Welt der Turmiten und Ameisen.

Literatur

• A.K. Dewdney: Turmiten, in: Immo Diener (Hg.): Computer-Kurzweil 2, Spektrum Akademischer Verlag: Verständliche Forschung, Heidelberg 1992, Seiten 156-160
• Ameise (Turingmaschine) in der Wikipedia.